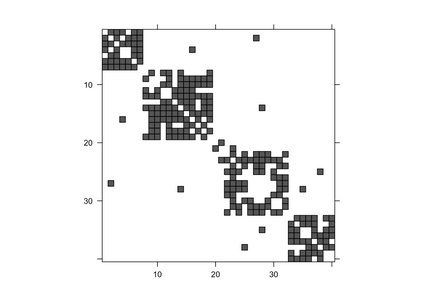
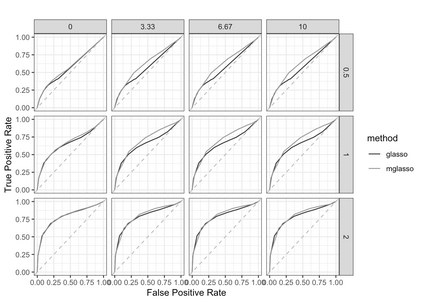
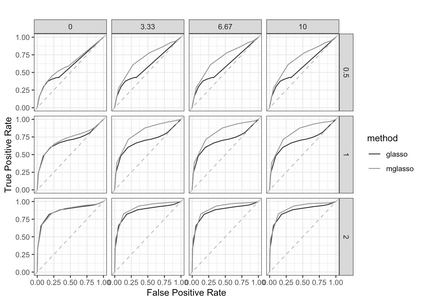
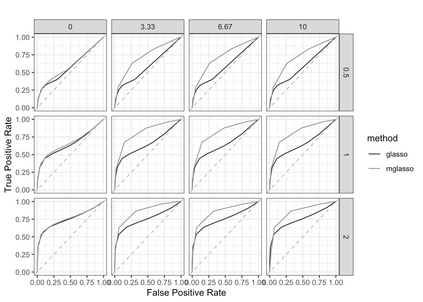
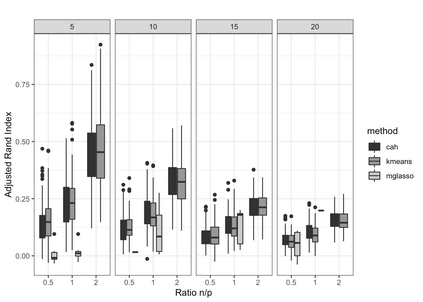
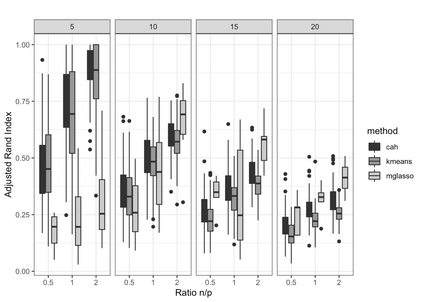
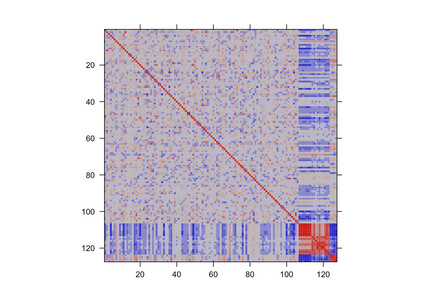
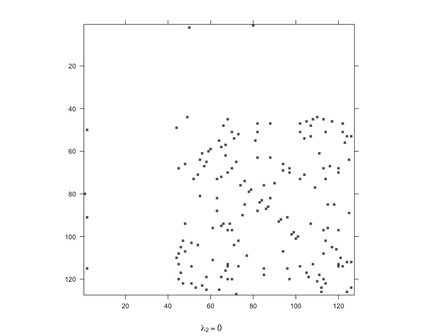
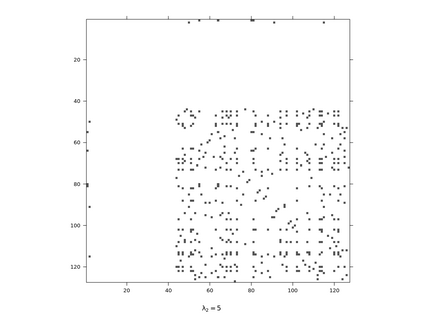
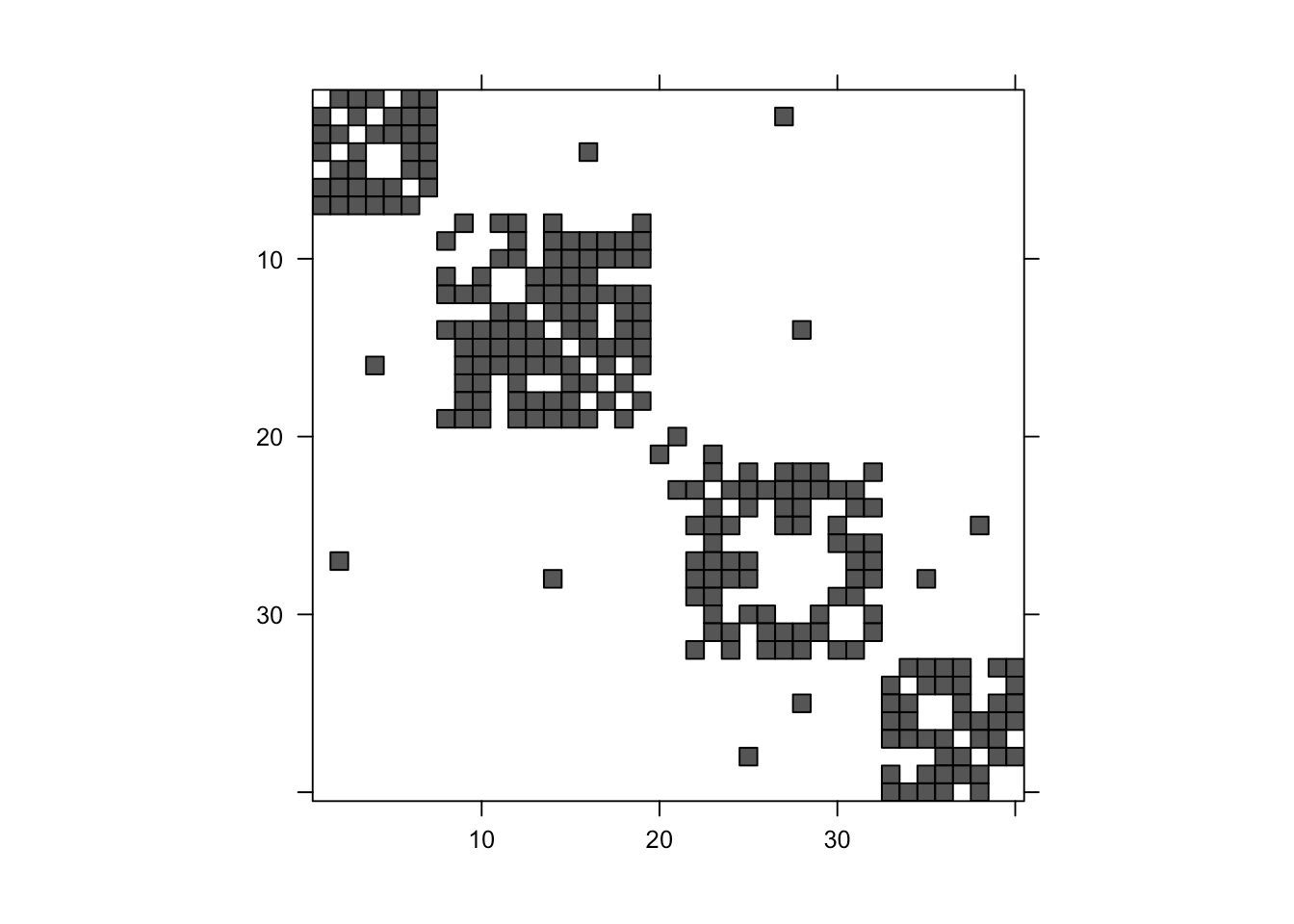
Gaussian Graphical Models (GGMs) are widely used for exploratory data analysis in various fields such as genomics, ecology, psychometry. In a high-dimensional setting, when the number of variables exceeds the number of observations by several orders of magnitude, the estimation of GGM is a difficult and unstable optimization problem. Clustering of variables or variable selection is often performed prior to GGM estimation. We propose a new method allowing to simultaneously infer a hierarchical clustering structure and the graphs describing the structure of independence at each level of the hierarchy. This method is based on solving a convex optimization problem combining a graphical lasso penalty with a fused type lasso penalty. Results on real and synthetic data are presented.
翻译:Gausian 图形模型(GGMS)被广泛用于基因组学、生态学、精神测量等各个领域的探索性数据分析。在高维环境中,当变量数量超过观测数量以几个数量级表示时,对GGM的估计是一个困难和不稳定的优化问题。变量或变量选择的分组往往在GGGM估算之前进行。我们建议了一种新的方法,允许同时推算等级分组结构和描述各级独立结构的图表。这种方法的基础是解决将图形拉索处罚与引信型拉索处罚相结合的二次曲线优化问题。我们介绍了关于真实和合成数据的结果。