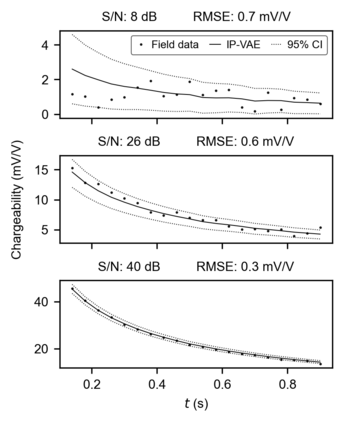
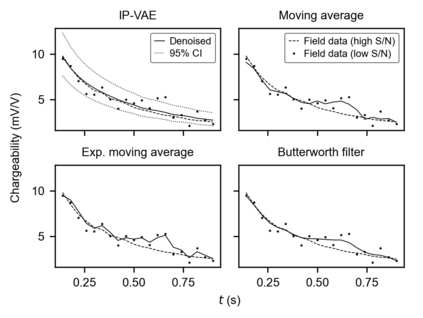
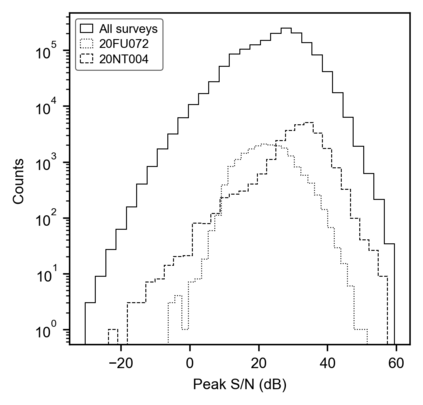
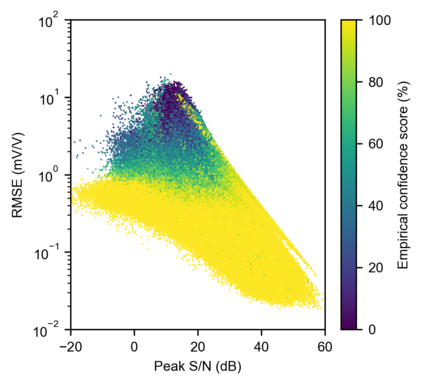
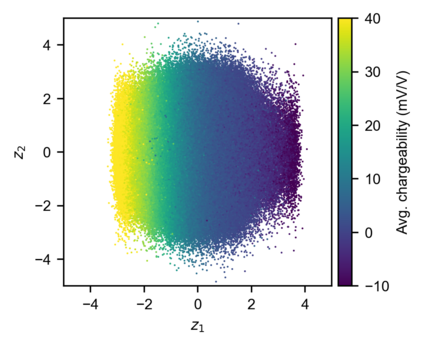
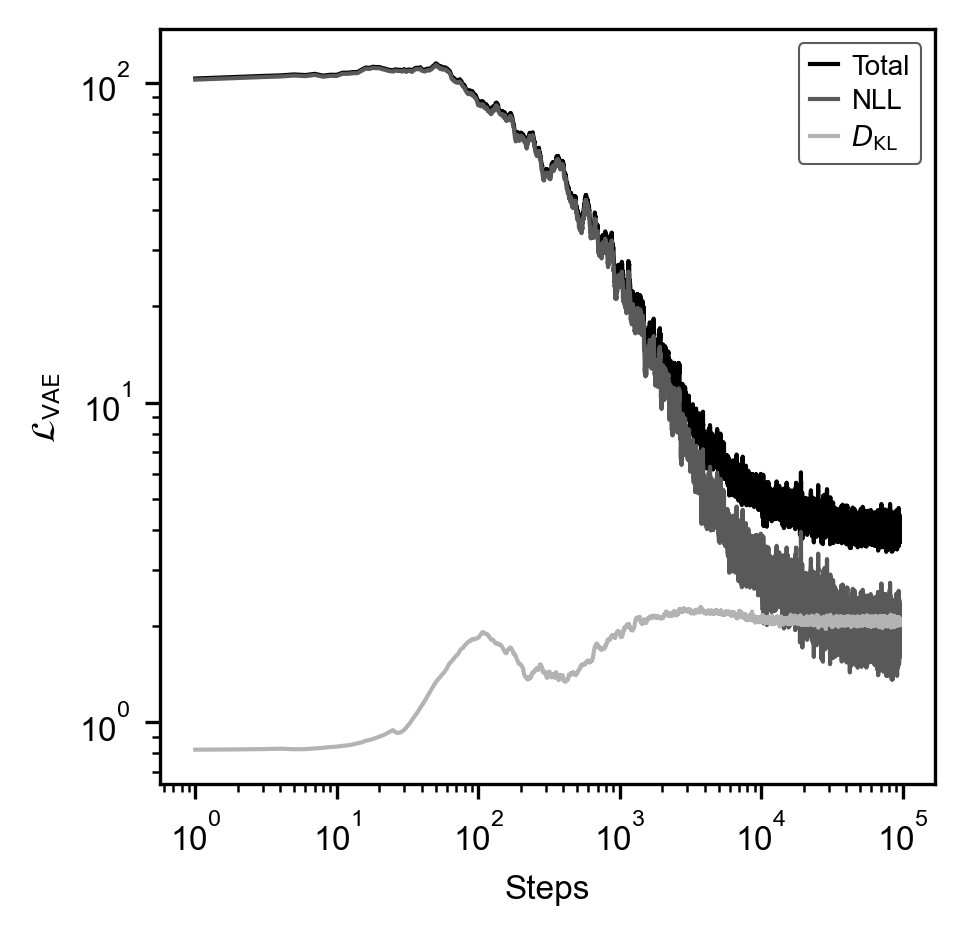
We present a novel approach for data-driven modeling of the time-domain induced polarization (IP) phenomenon using variational autoencoders (VAE). VAEs are Bayesian neural networks that aim to learn a latent statistical distribution to encode extensive data sets as lower dimension representations. We collected 1 600 319 IP decay curves in various regions of Canada, the United States and Kazakhstan, and compiled them to train a deep VAE. The proposed deep learning approach is strictly unsupervised and data-driven: it does not require manual processing or ground truth labeling of IP data. Moreover, our VAE approach avoids the pitfalls of IP parametrization with the empirical Cole-Cole and Debye decomposition models, simple power-law models, or other sophisticated mechanistic models. We demonstrate four applications of VAEs to model and process IP data: (1) representative synthetic data generation, (2) unsupervised Bayesian denoising and data uncertainty estimation, (3) quantitative evaluation of the signal-to-noise ratio, and (4) automated outlier detection. We also interpret the IP compilation's latent representation and reveal a strong correlation between its first dimension and the average chargeability of IP decays. Finally, we experiment with varying VAE latent space dimensions and demonstrate that a single real-valued scalar parameter contains sufficient information to encode our extensive IP data compilation. This new finding suggests that modeling time-domain IP data using mathematical models governed by more than one free parameter is ambiguous, whereas modeling only the average chargeability is justified. A pre-trained implementation of our model -- readily applicable to new IP data from any geolocation -- is available as open-source Python code for the applied geophysics community.
翻译:我们用变式自动电解码器(VAE)对时间驱动的极化(IP)现象的数据驱动建模提出了一种新颖的方法。 VAE是巴伊西亚神经网络,目的是学习隐性统计分布,将广泛的数据集编码为较低尺寸表示法。我们在加拿大、美国和哈萨克斯坦各地区收集了1,600319个IP衰变曲线,并汇编了这些曲线以培训深层VAE。提议的深层次学习方法严格不受监督,数据驱动:它不需要对IP数据进行数学处理或地面真实标记。此外,我们的VAE方法避免了IP超常化的陷阱,而根据经验性Cole和Debye分解模型或其他复杂的机械模型,我们在加拿大、美国和哈萨克斯坦各地区收集了1,600319个IP衰变曲线曲线曲线曲线,用来对模型进行深入的模拟数据生成和数据。 (b) Bayesian 模型失常模型和数据不确定性估算, (bisalian) 定量评估, IP-ral-ror-rent 比率比率比,以及自动外检测。我们还将IP 应用的IP 的IPI-co值数据汇编用于一个深度数据缩缩缩缩化, 显示最终的精确度, 和直观, 显示一个空间数据缩缩缩化数据化数据流的精确度,显示我们使用一个可比较的精确度的精确度的精确度的精确度。
相关内容
- Today (iOS and OS X): widgets for the Today view of Notification Center
- Share (iOS and OS X): post content to web services or share content with others
- Actions (iOS and OS X): app extensions to view or manipulate inside another app
- Photo Editing (iOS): edit a photo or video in Apple's Photos app with extensions from a third-party apps
- Finder Sync (OS X): remote file storage in the Finder with support for Finder content annotation
- Storage Provider (iOS): an interface between files inside an app and other apps on a user's device
- Custom Keyboard (iOS): system-wide alternative keyboards
Source: iOS 8 Extensions: Apple’s Plan for a Powerful App Ecosystem