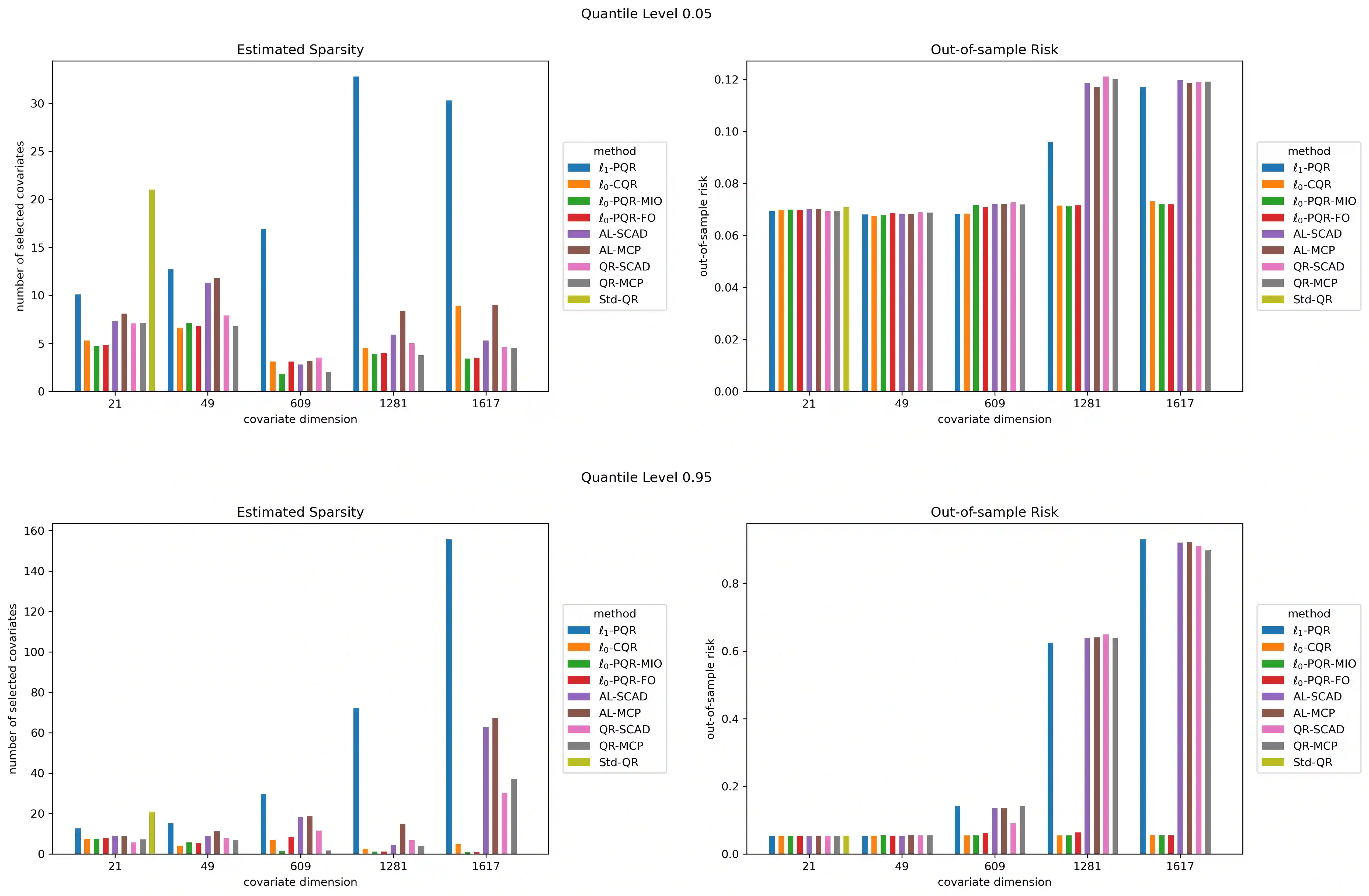
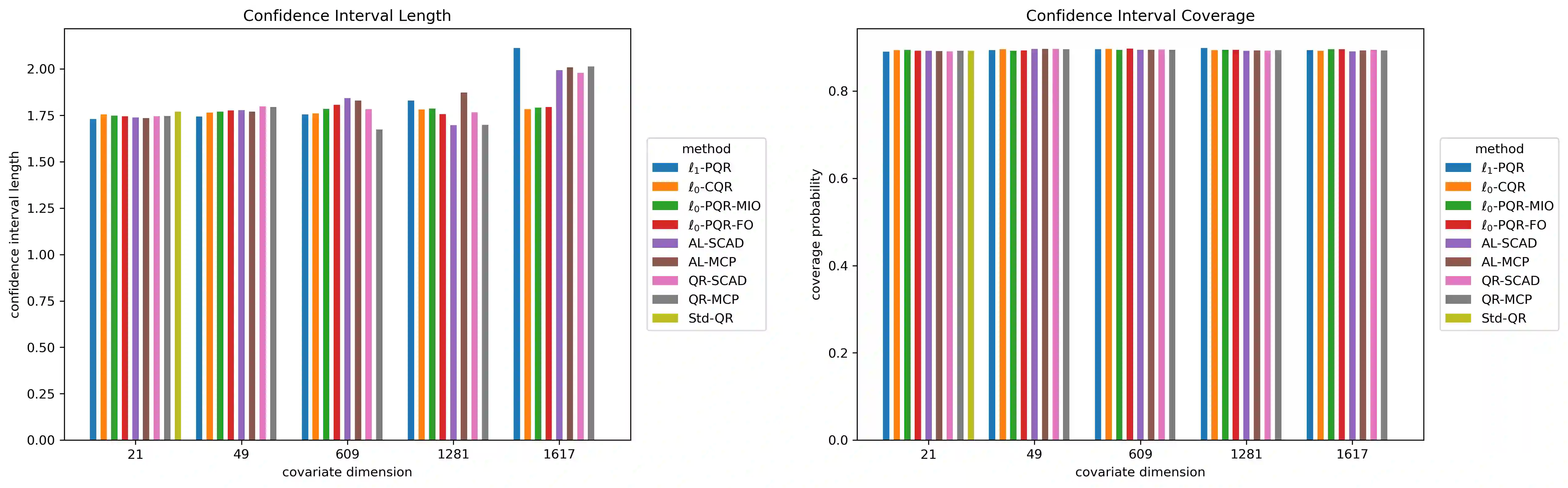
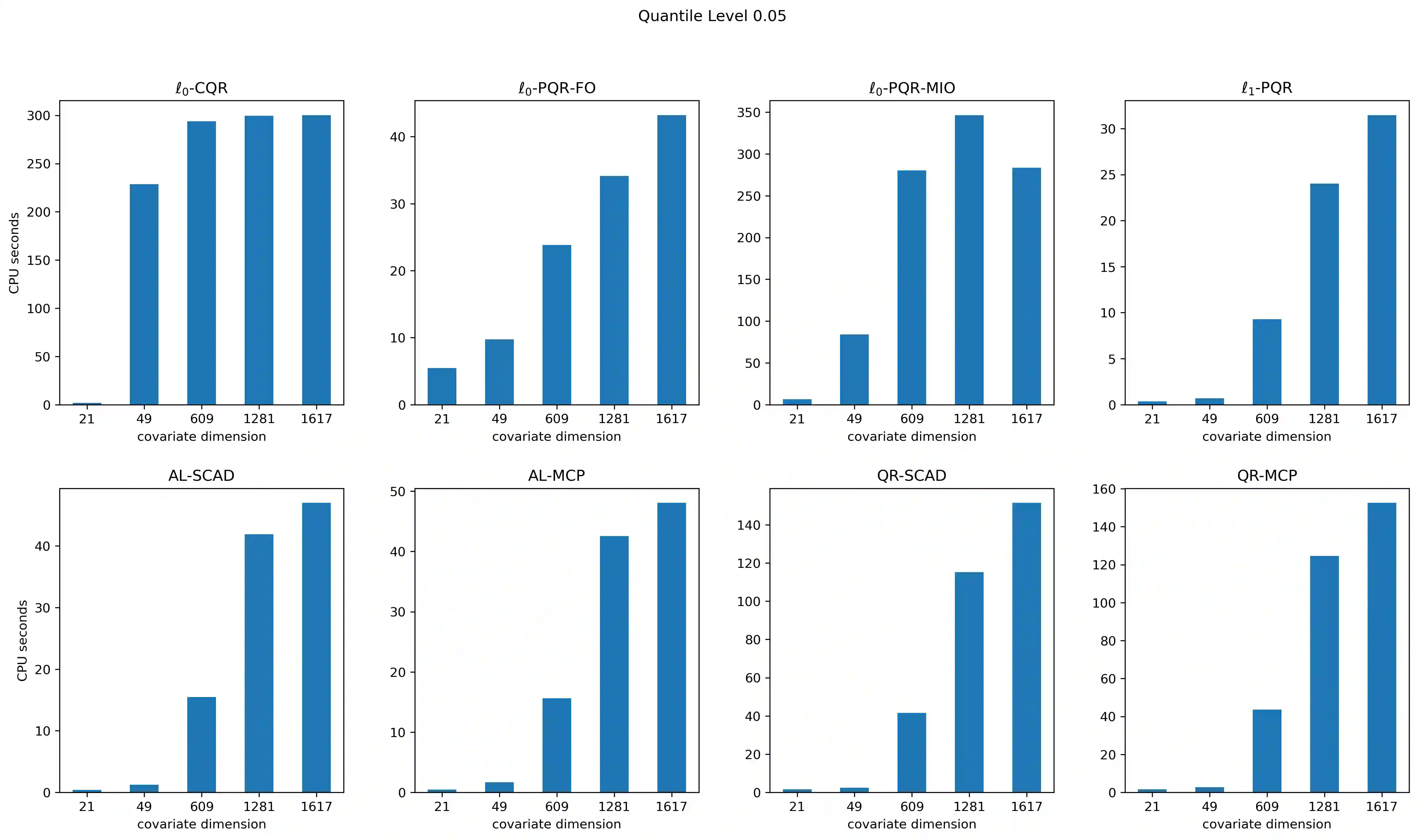
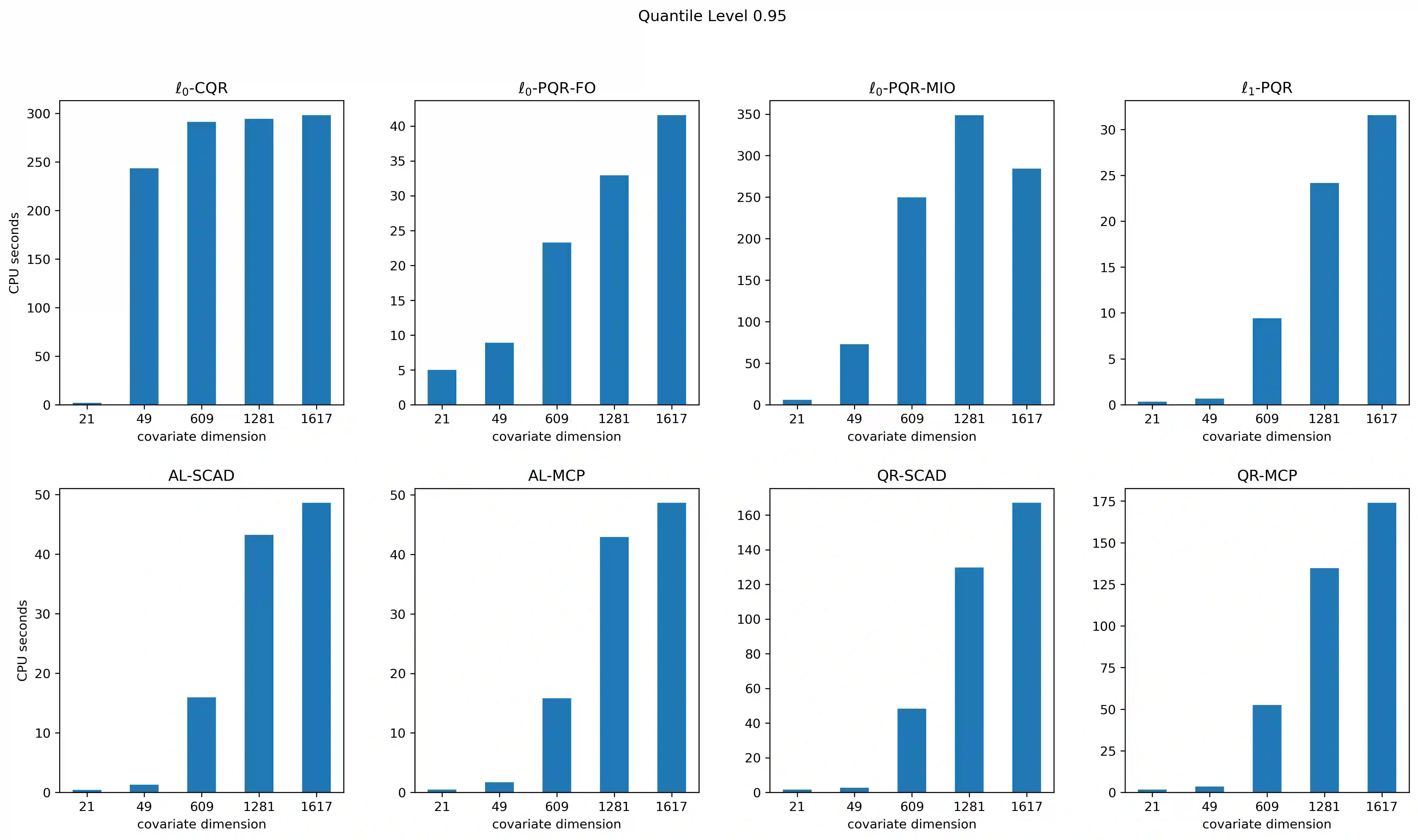
We consider both $\ell _{0}$-penalized and $\ell _{0}$-constrained quantile regression estimators. For the $\ell _{0}$-penalized estimator, we derive an exponential inequality on the tail probability of excess quantile prediction risk and apply it to obtain non-asymptotic upper bounds on the mean-square parameter and regression function estimation errors. We also derive analogous results for the $\ell _{0}$-constrained estimator. The resulting rates of convergence are nearly minimax-optimal and the same as those for $\ell _{1}$-penalized and non-convex penalized estimators. Further, we characterize expected Hamming loss for the $\ell _{0}$-penalized estimator. We implement the proposed procedure via mixed integer linear programming and also a more scalable first-order approximation algorithm. We illustrate the finite-sample performance of our approach in Monte Carlo experiments and its usefulness in a real data application concerning conformal prediction of infant birth weights (with $n\approx 10^{3}$ and up to $p>10^{3}$). In sum, our $\ell _{0}$-based method produces a much sparser estimator than the $\ell _{1}$-penalized and non-convex penalized approaches without compromising precision.
翻译:我们既考虑美元=0.0美元,也考虑美元=0.0美元; 美元=0.0美元; 美元=0.0美元; 受约束的四分位回归估计估计值。 对于美元=0.0美元; 美元=0.0美元; 受处罚的估算值,我们从超四分位预测风险的尾端概率上得出指数不平等性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数性指数。