SoftIGA: soft isogeometric analysis

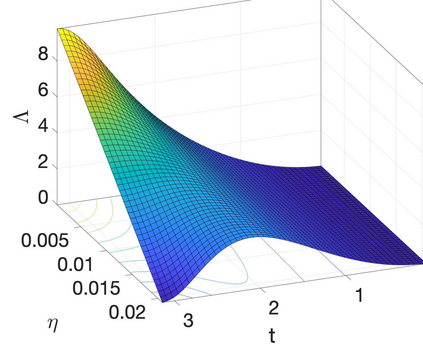
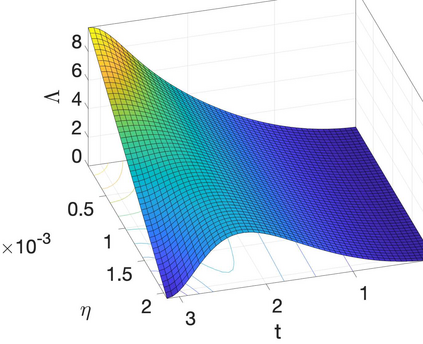
We extend the softFEM idea to isogeometric analysis (IGA) to reduce the stiffness (consequently, the condition numbers) of the IGA discretized problem. We refer to the resulting approximation technique as softIGA. We obtain the resulting discretization by first removing the IGA spectral outliers to reduce the system's stiffness. We then add high-order derivative-jump penalization terms (with negative penalty parameters) to the standard IGA bilinear forms. The penalty parameter seeks to minimize spectral/dispersion errors while maintaining the coercivity of the bilinear form. We establish dispersion errors for both outlier-free IGA (OF-IGA) and softIGA elements. We also derive analytical eigenpairs for the resulting matrix eigenvalue problems and show that the stiffness and condition numbers of the IGA systems significantly improve (reduce). We prove a superconvergent result of order $h^{2p+4}$ for eigenvalues where $h$ characterizes the mesh size and $p$ specifies the order of the B-spline basis functions. To illustrate the main idea and derive the analytical results, we focus on uniform meshes in 1D and tensor-product meshes in multiple dimensions. For the eigenfunctions, softIGA delivers the same optimal convergence rates as the standard IGA approximation. Various numerical examples demonstrate the advantages of softIGA over IGA.