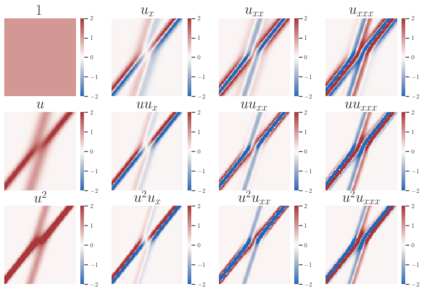
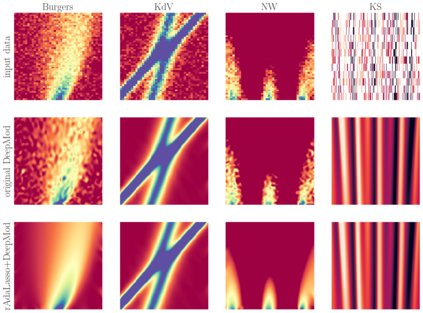
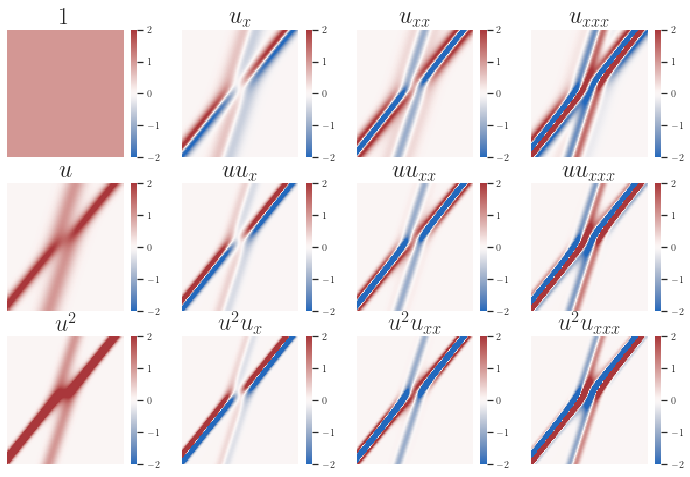
Discovering the partial differential equations underlying spatio-temporal datasets from very limited and highly noisy observations is of paramount interest in many scientific fields. However, it remains an open question to know when model discovery algorithms based on sparse regression can actually recover the underlying physical processes. In this work, we show the design matrices used to infer the equations by sparse regression can violate the irrepresentability condition (IRC) of the Lasso, even when derived from analytical PDE solutions (i.e. without additional noise). Sparse regression techniques which can recover the true underlying model under violated IRC conditions are therefore required, leading to the introduction of the randomised adaptive Lasso. We show once the latter is integrated within the deep learning model discovery framework DeepMod, a wide variety of nonlinear and chaotic canonical PDEs can be recovered: (1) up to $\mathcal{O}(2)$ higher noise-to-sample ratios than state-of-the-art algorithms, (2) with a single set of hyperparameters, which paves the road towards truly automated model discovery.
翻译:在许多科学领域,从非常有限和高度吵闹的观测中发现片段时空数据集的局部差分方程式是最重要的。然而,对于许多科学领域来说,仍是一个有待解决的问题,以了解基于微弱回归的模型发现算法何时能够真正恢复基本物理过程。在这项工作中,我们展示了用于通过稀薄回归推断等式的设计矩阵,即使从分析性的PDE解决方案(即无额外噪音)中得出,也有可能违反Lasso的不可代表性条件(IRC) 。因此,需要粗糙回归技术,在被破坏的IRC条件下能够恢复真实的基本模型,从而导致引入随机的适应性拉索。一旦将后者纳入深层次学习模型发现框架DeepMod,我们就会显示,大量非线性和混乱的卡通式PDE可以被恢复:(1) 高达 $mathcal{O}(2) 美元, 高于状态-艺术算法,(2) 使用单一的超立方计,为真正自动化模型发现铺设道路的路径。