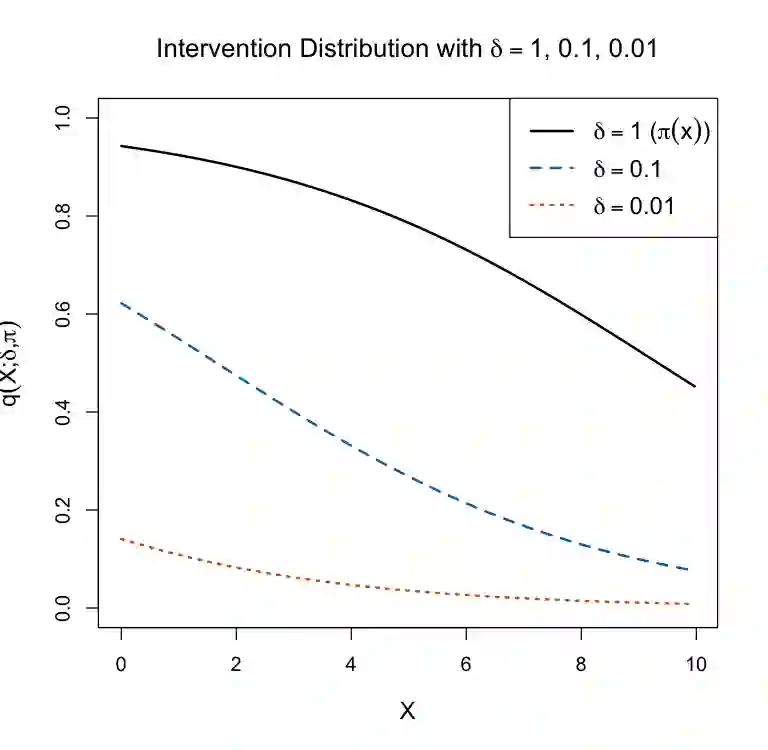
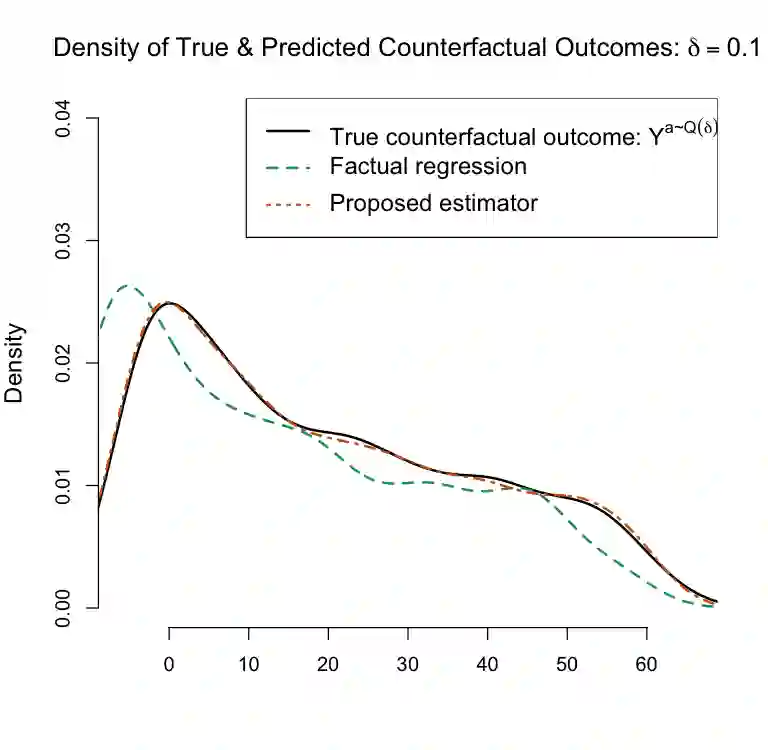
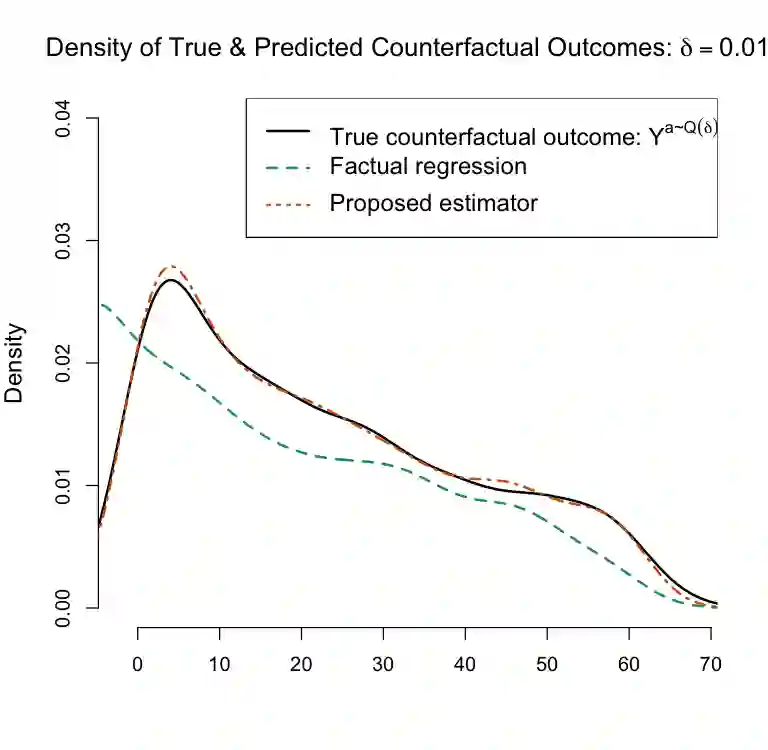
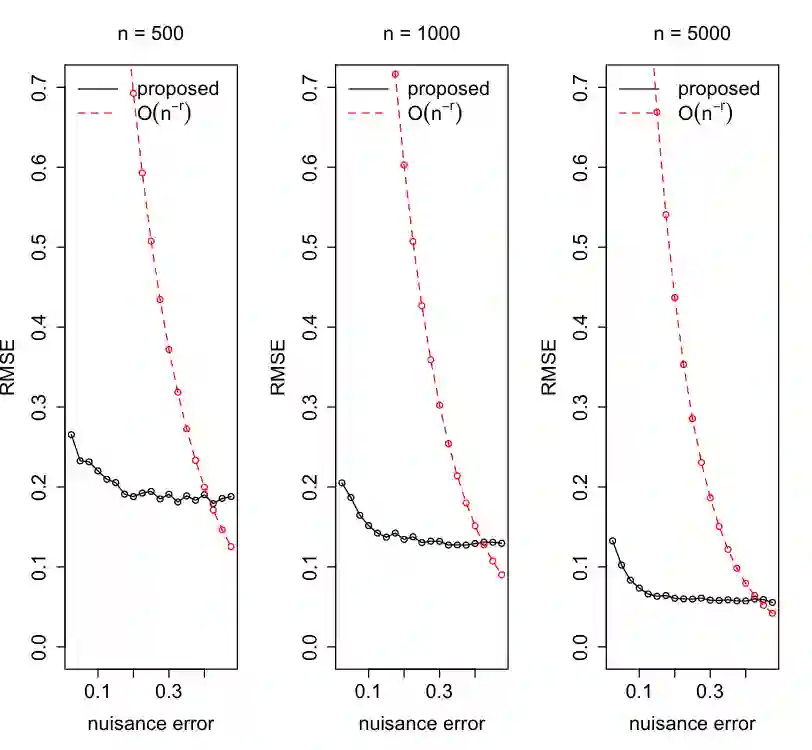
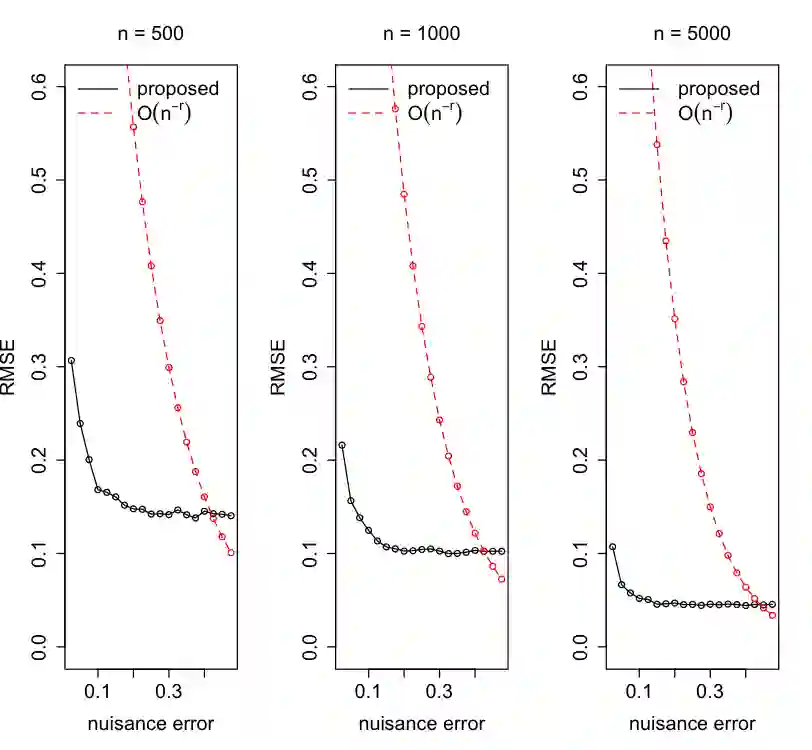
We study counterfactual regression, which aims to map input features to outcomes under hypothetical scenarios that differ from those observed in the data. This is particularly useful for decision-making when adapting to sudden shifts in treatment patterns is essential. We propose a doubly robust-style estimator for counterfactual regression within a generalizable framework that accommodates a broad class of risk functions and flexible constraints, drawing on tools from semiparametric theory and stochastic optimization. Our approach uses incremental interventions to enhance adaptability while maintaining consistency with standard methods. We formulate the target estimand as the optimal solution to a stochastic optimization problem and develop an efficient estimation strategy, where we can leverage rapid development of modern optimization algorithms. We go on to analyze the rates of convergence and characterize the asymptotic distributions. Our analysis shows that the proposed estimators can achieve $\sqrt{n}$-consistency and asymptotic normality for a broad class of problems. Numerical illustrations highlight their effectiveness in adapting to unseen counterfactual scenarios while maintaining parametric convergence rates.
翻译:暂无翻译