On Low Field Size Constructions of Access-Optimal Convertible Codes

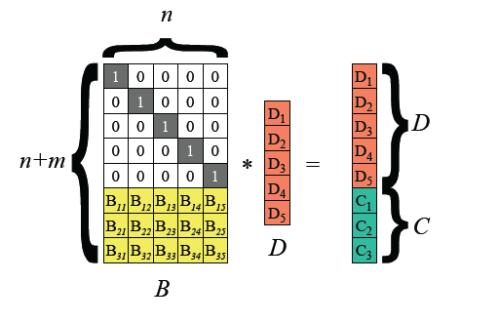
Most large-scale storage systems employ erasure coding to provide resilience against disk failures. Recent work has shown that tuning this redundancy to changes in disk failure rates leads to substantial storage savings. This process requires code conversion, wherein data encoded using an $[n^{I\mskip-2mu},k^{I\mskip-2mu}]$ initial code has to be transformed into data encoded using an $[n^{F\mskip-2mu},k^{F\mskip-2mu}]$ final code, a resource-intensive operation. Convertible codes are a class of codes that enable efficient code conversion while maintaining other desirable properties. In this paper, we focus on the access cost of conversion (total number of code symbols accessed in the conversion process) and on an important subclass of conversions known as the merge regime (combining multiple initial codewords into a single final codeword). In this setting, explicit constructions are known for systematic access-optimal Maximum Distance Separable (MDS) convertible codes for all parameters in the merge regime. However, the existing construction for a key subset of these parameters, which makes use of Vandermonde parity matrices, requires a large field size making it unsuitable for practical applications. In this paper, we provide (1) sharper bounds on the minimum field size requirement for such codes, and (2) explicit constructions for low field sizes for several parameter ranges. In doing so, we provide a proof of super-regularity of specially designed classes of Vandermonde matrices that could be of independent interest.