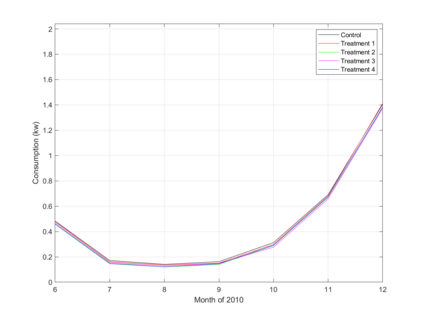
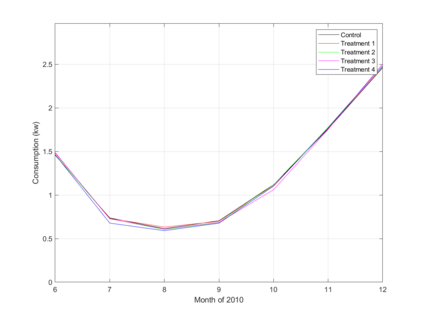
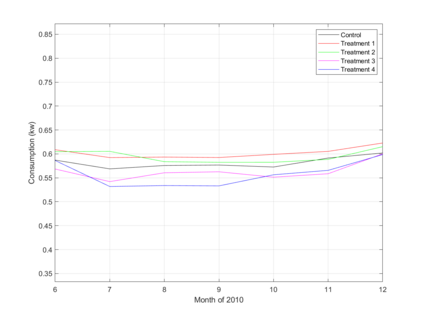
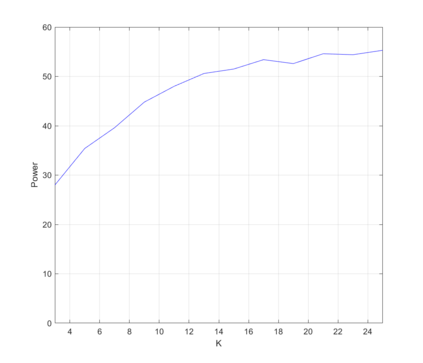
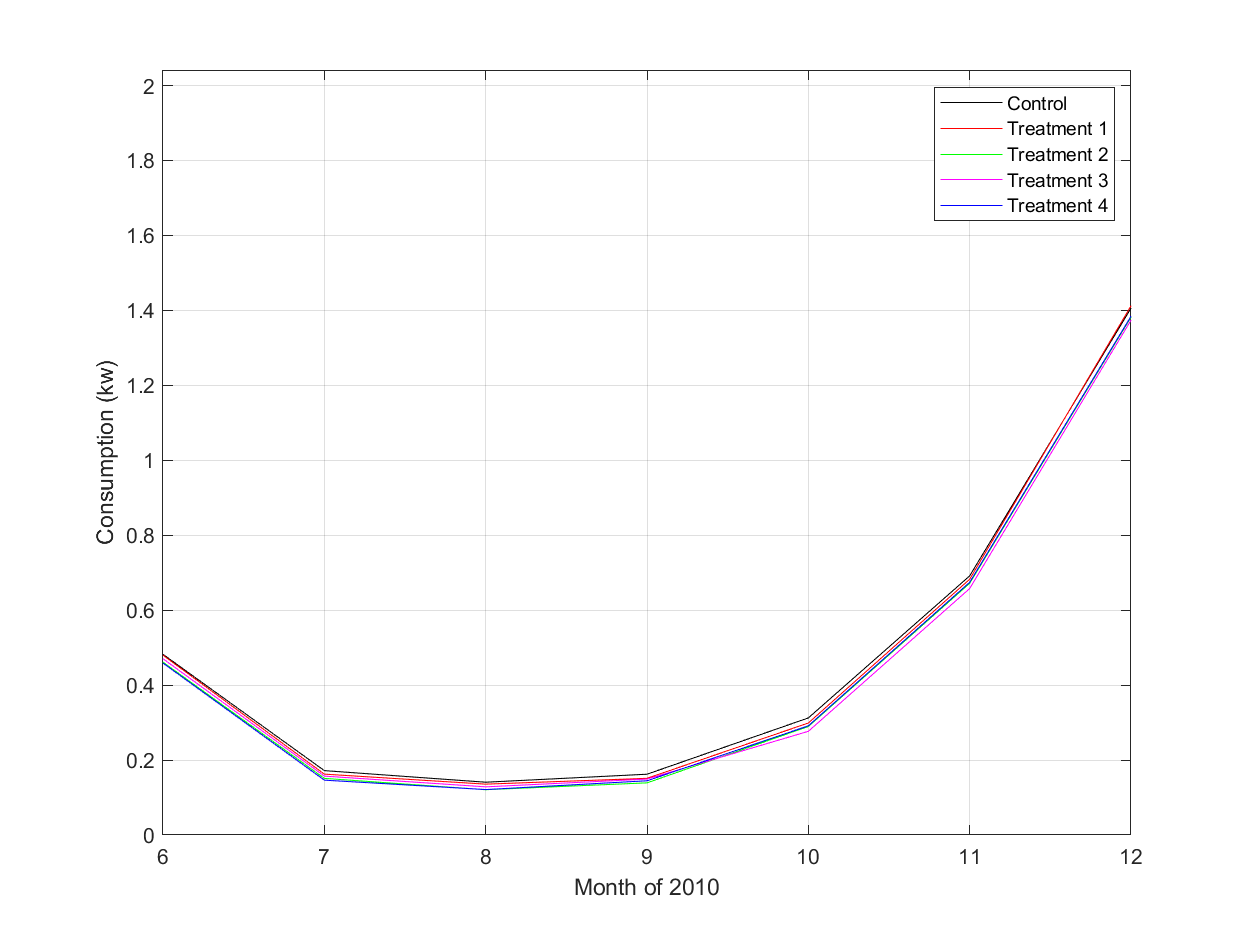
Economic data are often generated by stochastic processes that take place in continuous time, though observations may occur only at discrete times. For example, electricity and gas consumption take place in continuous time. Data generated by a continuous time stochastic process are called functional data. This paper is concerned with comparing two or more stochastic processes that generate functional data. The data may be produced by a randomized experiment in which there are multiple treatments. The paper presents a method for testing the hypothesis that the same stochastic process generates all the functional data. The test described here applies to both functional data and multiple treatments. It is implemented as a combination of two permutation tests. This ensures that in finite samples, the true and nominal probabilities that each test rejects a correct null hypothesis are equal. The paper presents upper and lower bounds on the asymptotic power of the test under alternative hypotheses. The results of Monte Carlo experiments and an application to an experiment on billing and pricing of natural gas illustrate the usefulness of the test.
翻译:经济数据往往是由连续时间进行的随机过程产生的,但观察可能只在不连续的时间进行,例如,电力和气体消耗是在连续的时间进行,连续时间的随机过程产生的数据称为功能性数据。本文涉及比较产生功能性数据的两种或两种以上随机过程;数据可能是通过有多种处理的随机实验产生的。本文提出了一个方法,用以测试同一随机过程产生所有功能性数据的假设。这里所述的试验既适用于功能性数据,也适用于多种处理。它作为两种变换试验的结合实施。这确保了在有限的样品中,每种试验拒绝正确的无效假设的真实和名义概率是相等的。本文在替代假设下对试验的无干扰能力作了上下限。Monte Carlo实验的结果以及对天然气计费和定价实验的应用说明了试验的效用。
相关内容
Source: Apple - iOS 8