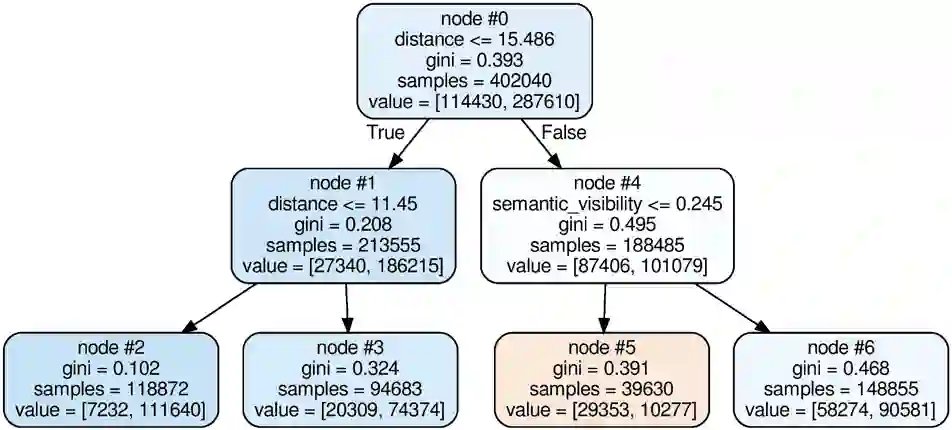
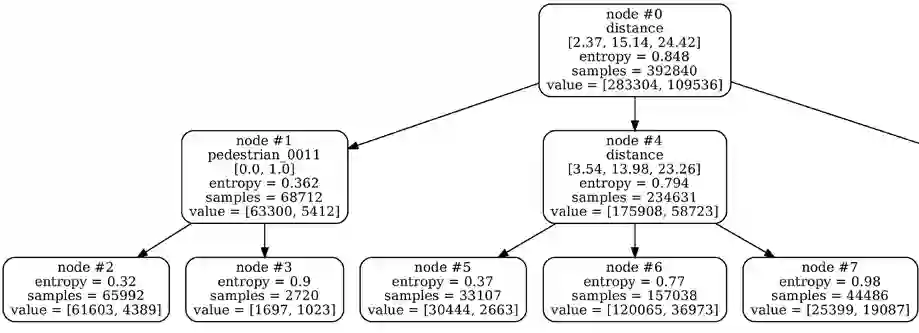
Outcomes of data-driven AI models cannot be assumed to be always correct. To estimate the uncertainty in these outcomes, the uncertainty wrapper framework has been proposed, which considers uncertainties related to model fit, input quality, and scope compliance. Uncertainty wrappers use a decision tree approach to cluster input quality related uncertainties, assigning inputs strictly to distinct uncertainty clusters. Hence, a slight variation in only one feature may lead to a cluster assignment with a significantly different uncertainty. Our objective is to replace this with an approach that mitigates hard decision boundaries of these assignments while preserving interpretability, runtime complexity, and prediction performance. Five approaches were selected as candidates and integrated into the uncertainty wrapper framework. For the evaluation based on the Brier score, datasets for a pedestrian detection use case were generated using the CARLA simulator and YOLOv3. All integrated approaches achieved a softening, i.e., smoothing, of uncertainty estimation. Yet, compared to decision trees, they are not so easy to interpret and have higher runtime complexity. Moreover, some components of the Brier score impaired while others improved. Most promising regarding the Brier score were random forests. In conclusion, softening hard decision tree boundaries appears to be a trade-off decision.
翻译:为估计这些结果的不确定性,提出了不确定性包装框架,其中考虑了与模型是否适合、投入质量和范围合规性有关的不确定性。 不确定性包装对集群输入质量相关不确定性采用决定树方法,严格将投入分配给不同的不确定性组。因此,只有一种特性略有不同,可能导致分组分配,不确定性大相径庭。我们的目标是用一种方法来取代这一方法,即减少这些任务难以决定的界限,同时保留可解释性、运行时间复杂性和预测性能。有五种方法被选为候选人,并被纳入不确定性包装框架。对于基于Brier评分的评价,使用CARLA模拟器和YOLOv3生成行人探测使用案例的数据集。所有综合方法都取得了软化,即平滑的不确定性估计。然而,与决策树相比,它们不容易解释,运行复杂性更高。此外,Brier评分的一些部分受损,而另一些部分则有所改善。关于Brier评分的多数有希望是随机的硬性森林。最后,关于Brier评分的硬性决定是软性森林。