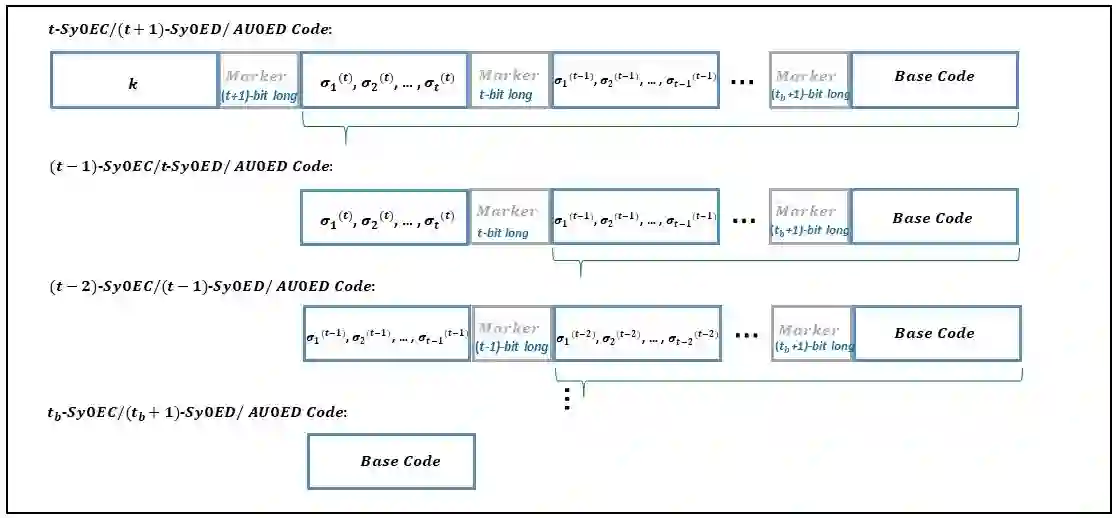
This paper gives some theory and efficient design of binary block systematic codes capable of controlling the deletions of the symbol ``$0$'' (referred to as $0$-deletions) and/or the insertions of the symbol ``$0$'' (referred to as $0$-insertions). The problem of controlling $0$-deletions and/or $0$-insertions (referred to as $0$-errors) is known to be equivalent to the efficient design of $L_{1}$ metric asymmetric error control codes over the natural alphabet, $\mathbb{N}$. So, $t$ $0$-insertion correcting codes can actually correct $t$ $0$-errors, detect $(t+1)$ $0$-errors and, simultaneously, detect all occurrences of only $0$-deletions or only $0$-insertions in every received word (briefly, they are $t$-Symmetric $0$-Error Correcting/$(t+1)$-Symmetric $0$-Error Detecting/All Unidirectional $0$-Error Detecting ($t$-Sy$0$EC/$(t+1)$-Sy$0$ED/AU$0$ED) codes). From the relations with the $L_{1}$ distance, optimal systematic code designs are given. In general, for all $t,k\in\mathbb{N}$, a recursive method is presented to encode $k$ information bits into efficient systematic $t$-Sy$0$EC/$(t+1)$-Sy$0$ED/AU$0$ED codes of length $$ n\leq k+t\log_{2}k+o(t\log n) $$ as $n\in\mathbb{N}$ increases. Decoding can be efficiently performed by algebraic means using the Extended Euclidean Algorithm (EEA).
翻译:本文给出了一些理论和高效设计, 用于控制符号“ 0美元” (简称为$0美元) 和(或) 符号“ 0美元” (简称为$美元插入 ) (简称为$美元插入 ) 。 控制 $- delet和(或) $- 美元插入( 称为$0美元 ) 的问题已知相当于 $ (美元) 的高效设计 美元, 美元, 美元, 美元, 美元 美元, 美元, 美元, 美元 美元, 美元 美元 。 美元, 美元 美元, 美元 美元, 美元 美元 美元, 美元 美元, 美元, 美元 美元 。 使用 美元 美元, 美元 美元, 以 美元 美元, 以 美元 美元 。 以 美元 美元, 以 美元 以 美元 美元, 以 以 美元 美元 以 美元, 以 美元 以 美元 以 美元 美元 以 以 美元 以 以 美元 以 以 美元 以 以 美元 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 美元 以 以 美元 以 以 以 以 以 美元 以 以 以 以 以 以 以 以 以 美元 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以