On Market Clearing of Day Ahead Auctions for European Power Markets: Cost Minimisation versus Social Welfare Maximisation

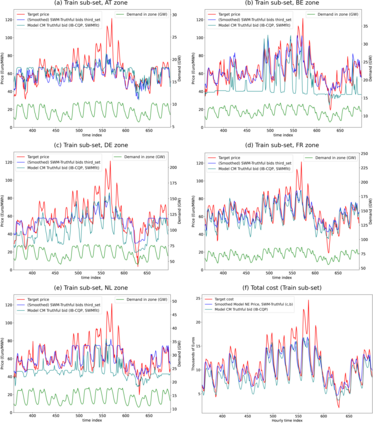
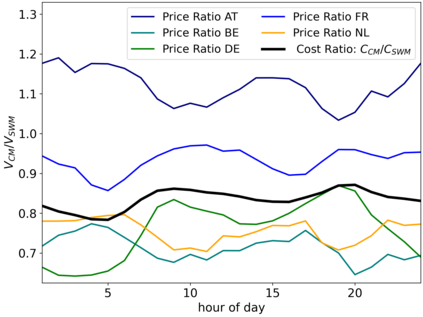
For the case of inflexible demand and considering network constraints, we introduce a Cost Minimisation (CM) based market clearing mechanism, and a model representing the standard Social Welfare Maximisation mechanism used in European Day Ahead Electricity Markets. Since the CM model corresponds to a more challenging optimisation problem, we propose four numerical algorithms that leverage the problem structure, each with different trade-offs between computational cost and convergence guarantees. These algorithms are evaluated on synthetic data to provide some intuition of their performance. We also provide strong (but partial) analytical results to facilitate efficient solution of the CM problem, which call for the introduction of a new concept: optimal zonal stack curves, and these results are used to devise one of the four solution algorithms. An evaluation of the CM and SWM models and their comparison is performed, under the assumption of truthful bidding, on the real world data of Central Western European Day Ahead Power Market during the period of 2019-2020. We show that the SWM model we introduce gives a good representation of the historical time series of the real prices. Further, the CM reduces the market power of producers, as generally this results in decreased zonal prices and always decreases the total cost of electricity procurement when compared to the currently employed SWM.