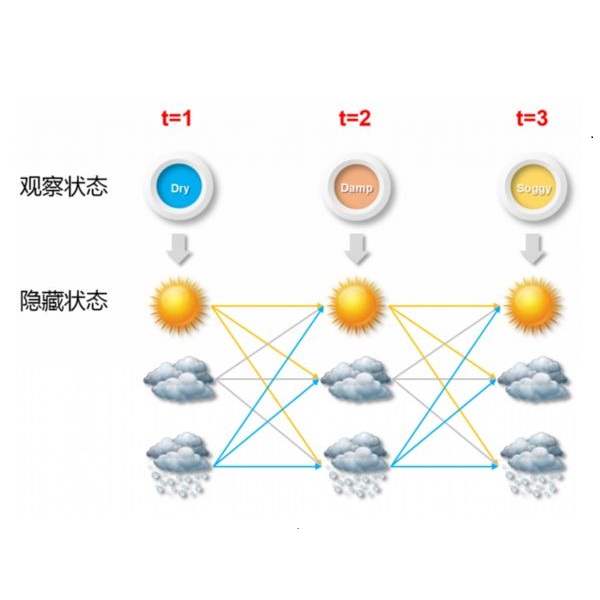
Given a nonparametric Hidden Markov Model (HMM) with two states, the question of constructing efficient multiple testing procedures is considered, treating one of the states as an unknown null hypothesis. A procedure is introduced, based on nonparametric empirical Bayes ideas, that controls the False Discovery Rate (FDR) at a user--specified level. Guarantees on power are also provided, in the form of a control of the true positive rate. One of the key steps in the construction requires supremum--norm convergence of preliminary estimators of the emission densities of the HMM. We provide the existence of such estimators, with convergence at the optimal minimax rate, for the case of a HMM with $J\ge 2$ states, which is of independent interest.
翻译:鉴于与两个州有非对称的隐藏马克夫模式(HMM),考虑建立高效的多重测试程序的问题,将其中一个州视为未知的无效假设;根据非对称经验性贝ys理念,引入了一个程序,在用户指定水平上控制假发现率(FDR),还以控制真实正率的形式提供权力保障;建设中的关键步骤之一要求HMM排放密度初步估计者达到最高标准-中枢。 我们提供这种估计者的存在,以最优的迷你速率统一,对于HMM和2美元州的情况,HMM和2美元是独立感兴趣的州。