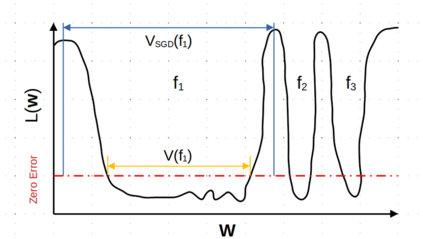
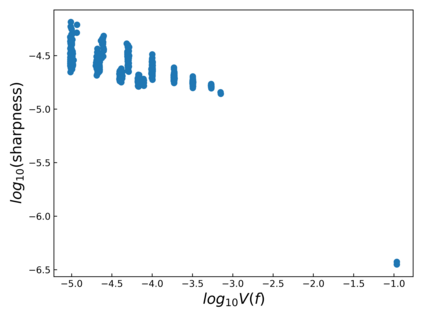
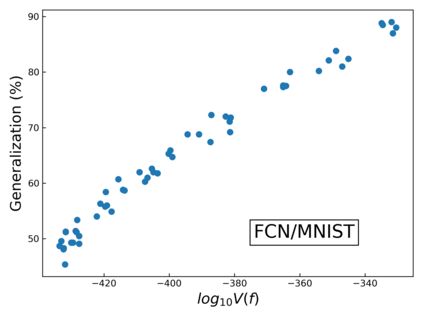
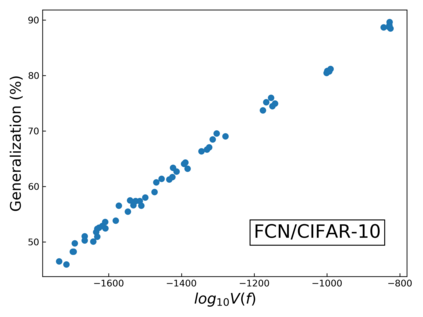
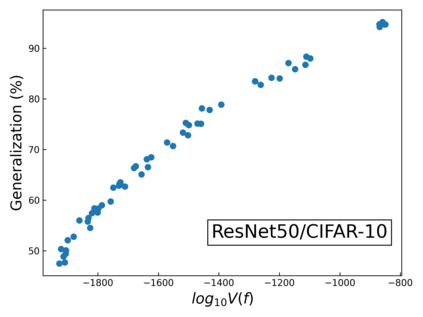
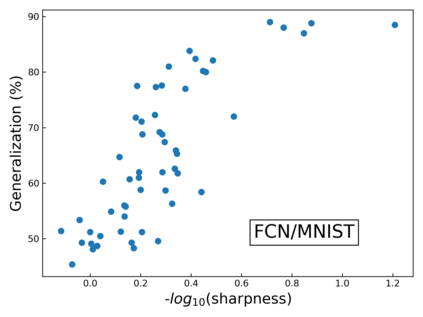
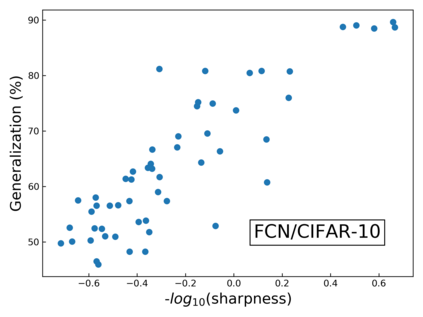
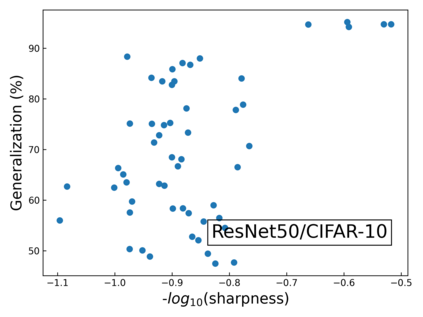
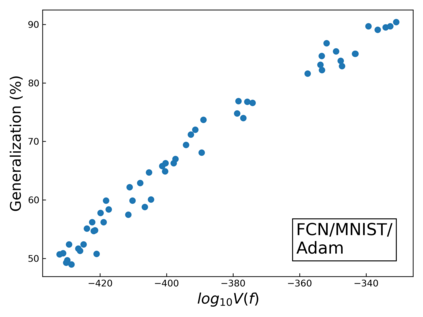
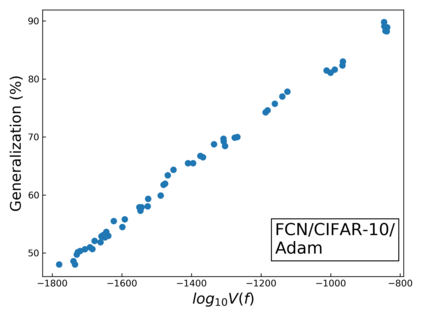
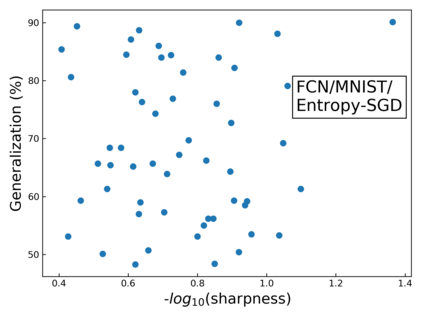
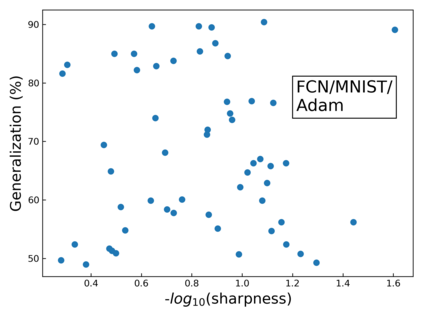
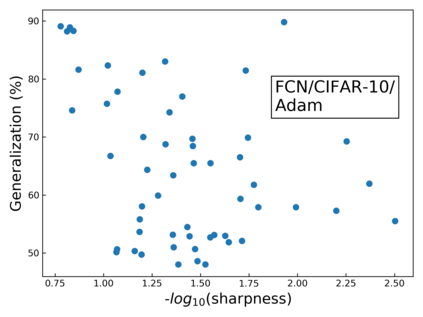
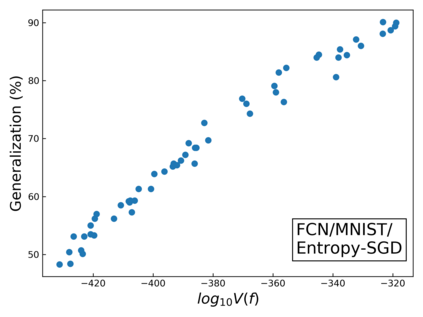
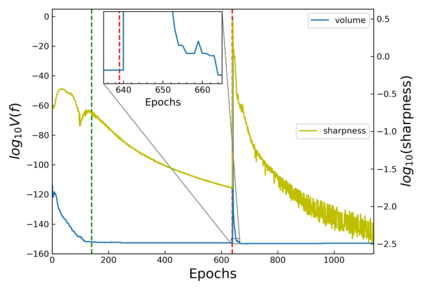
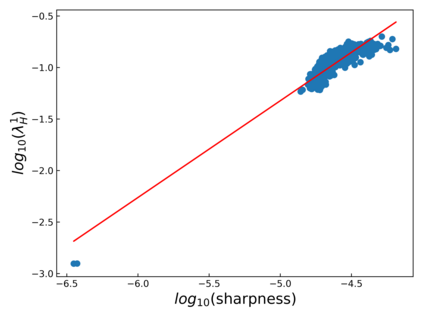
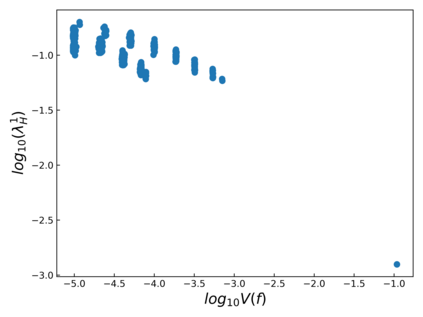
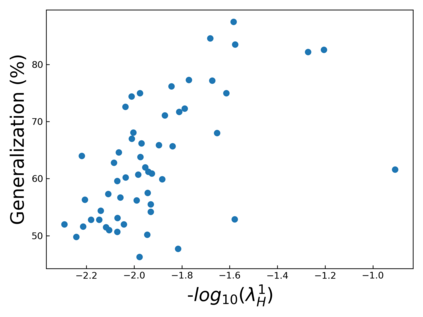
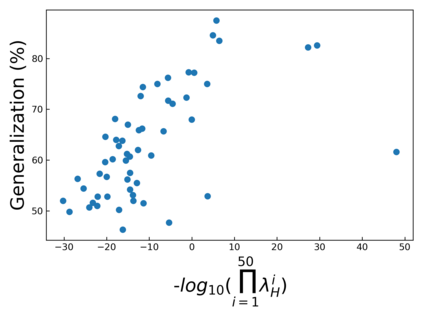
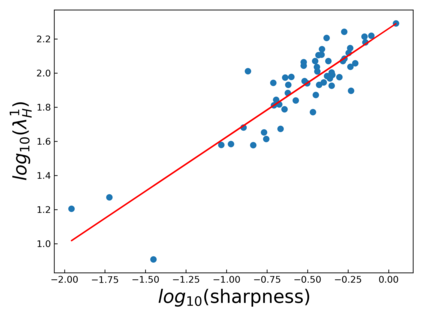
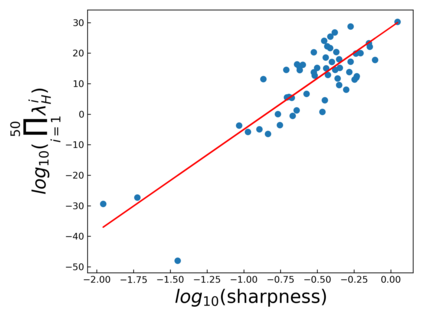
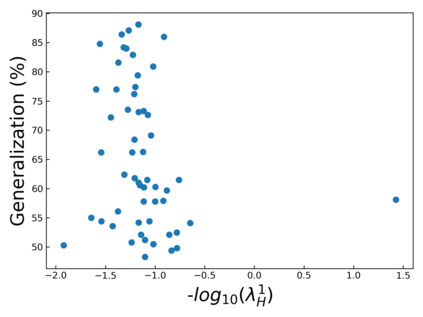
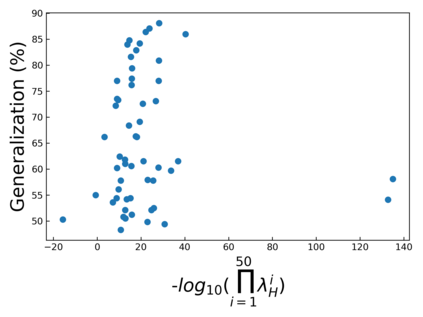
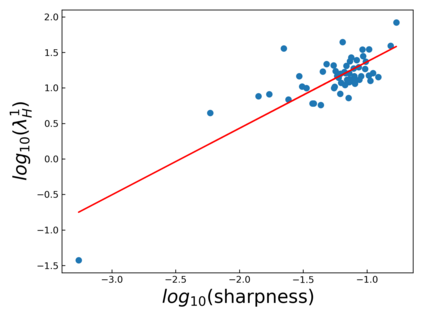
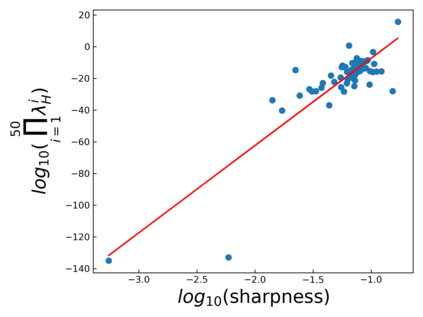
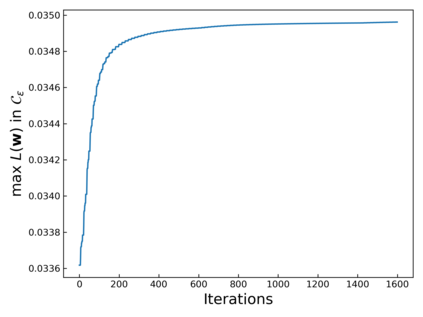
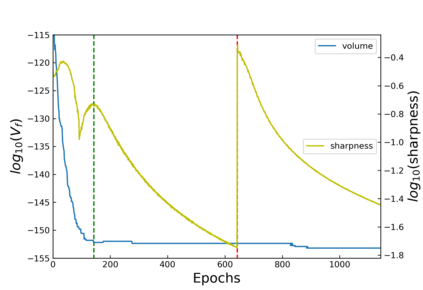
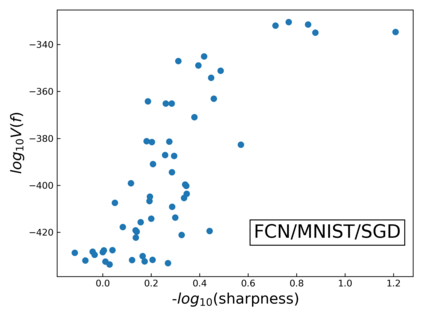
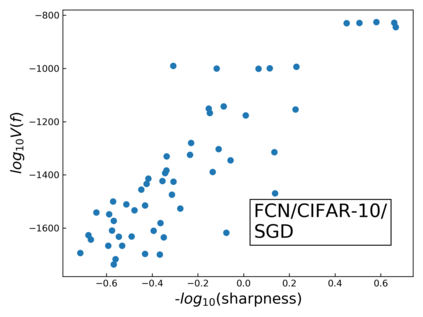
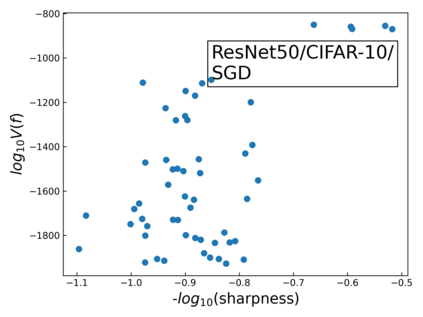
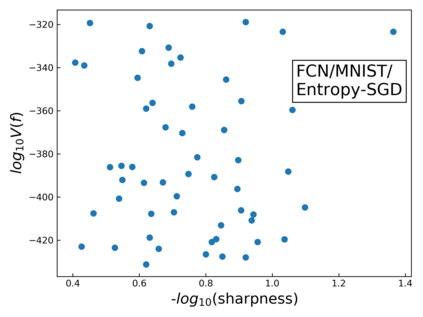
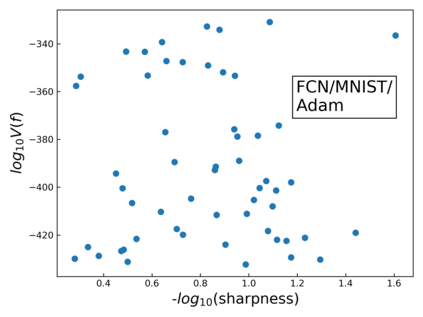
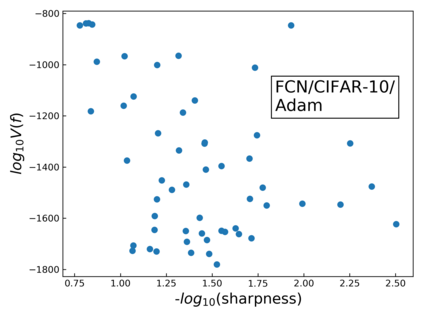
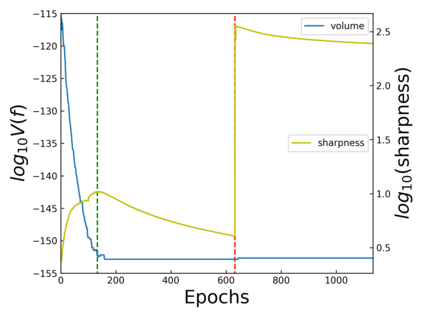
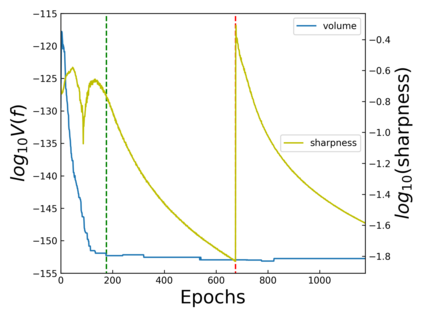
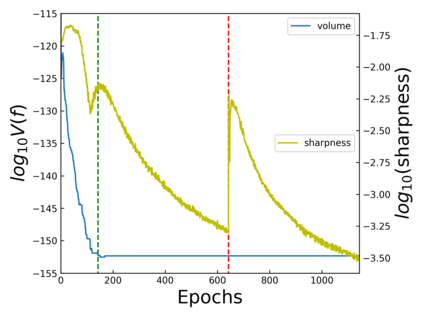
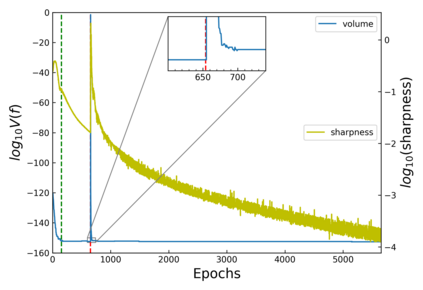
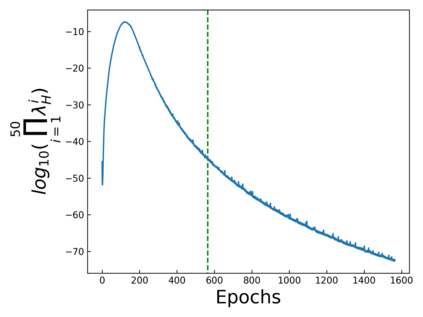
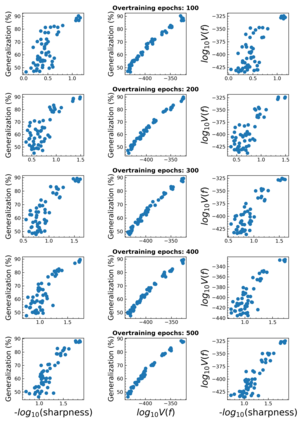
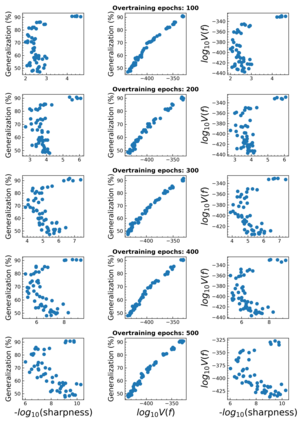
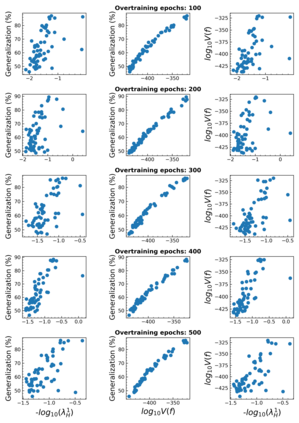
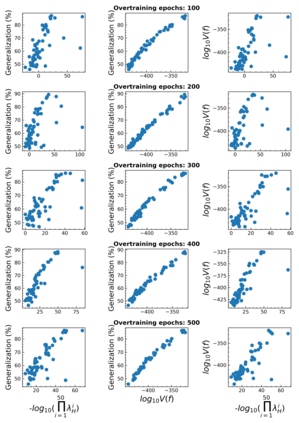
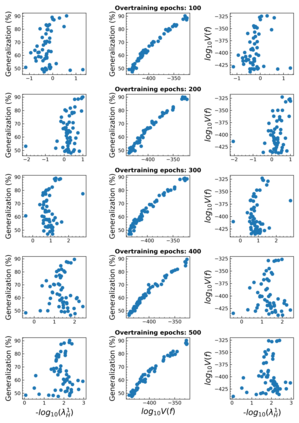
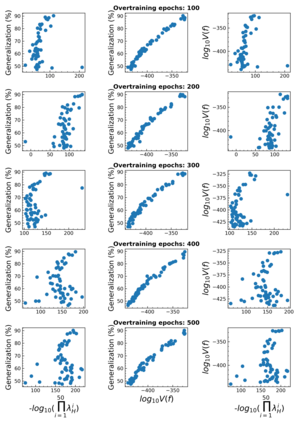
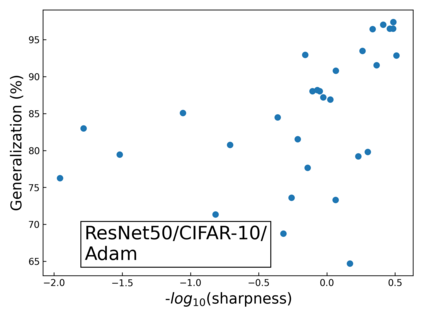
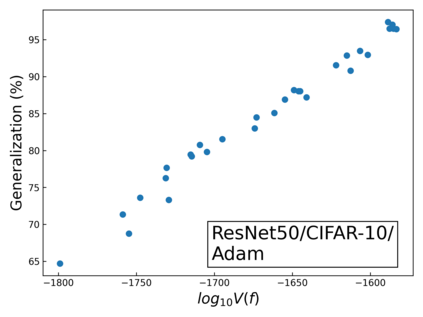
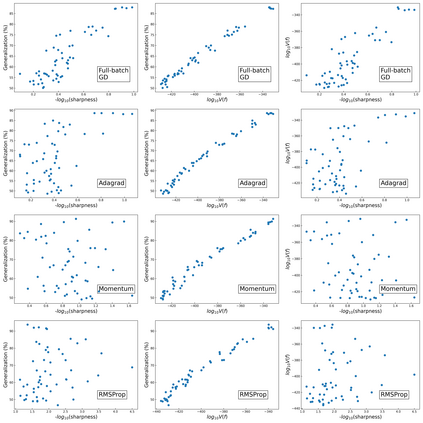
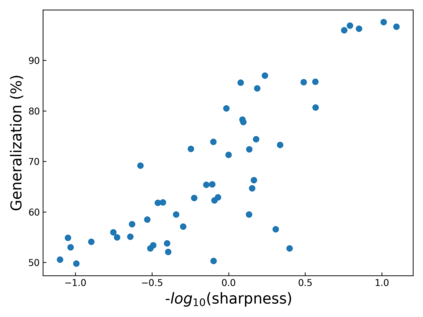
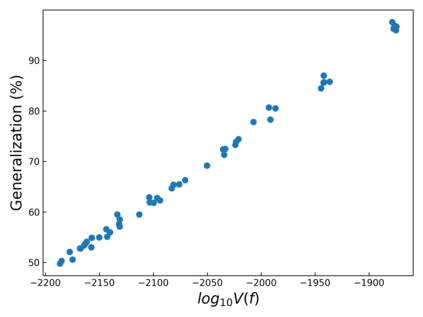
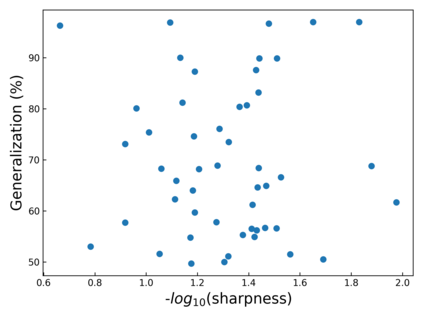
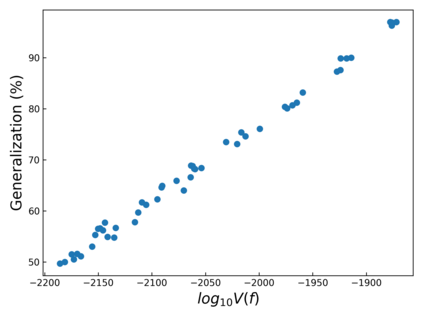
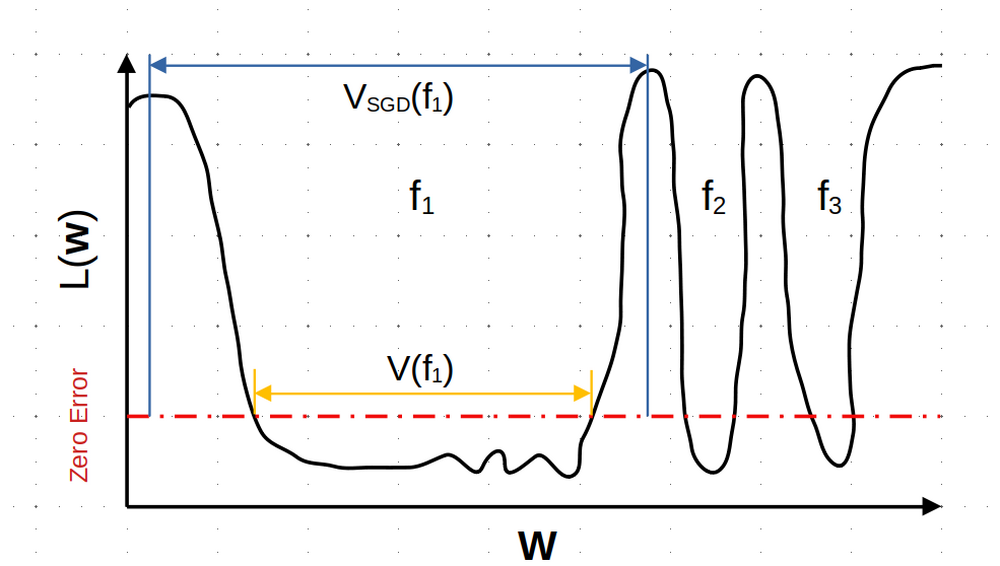
The intuition that local flatness of the loss landscape is correlated with better generalization for deep neural networks (DNNs) has been explored for decades, spawning many different local flatness measures. Here we argue that these measures correlate with generalization because they are local approximations to a global property, the volume of the set of parameters mapping to a specific function. This global volume is equivalent to the Bayesian prior upon initialization. For functions that give zero error on a test set, it is directly proportional to the Bayesian posterior, making volume a more robust and theoretically better grounded predictor of generalization than flatness. Whilst flatness measures fail under parameter re-scaling, volume remains invariant and therefore continues to correlate well with generalization. Moreover, some variants of SGD can break the flatness-generalization correlation, while the volume-generalization correlation remains intact.
翻译:损失场景的局部平坦性与对深神经网络(DNNs)的更好概括化相关联的直觉已经探索了几十年,从而产生了许多不同的局部平坦度测量标准。 我们在这里争论说,这些措施与一般化相关,因为它们是全球财产的局部近似值,是一组参数绘图的体积与特定函数。这个全球量相当于启动前的巴伊西亚体积。对于测试组零误差的功能来说,它直接与巴耶斯海脊脊柱成正比,使体积成为比平坦更稳健的、在理论上更有依据的通用预测。 虽然在参数再缩放下,平度度度测量不成功,但体积仍然不易变,因此继续与一般化密切相关。 此外,SGD的某些变量可以打破平坦性一般化的关联,而数量一般化的关联则保持不变。