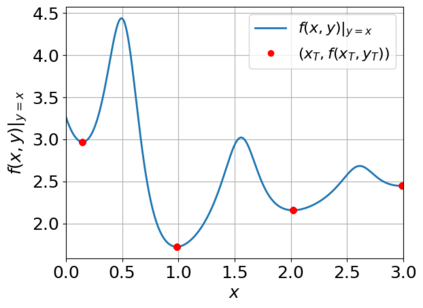
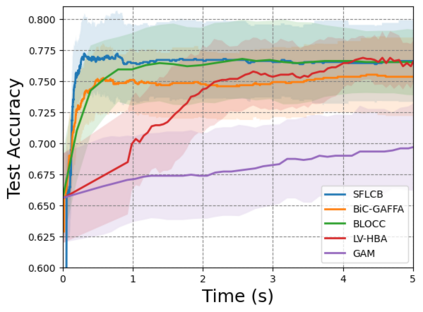
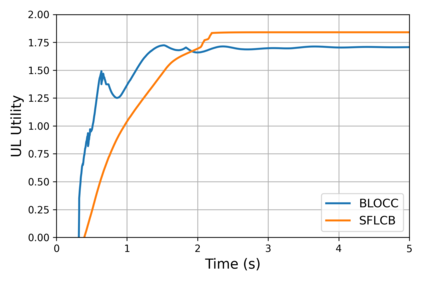
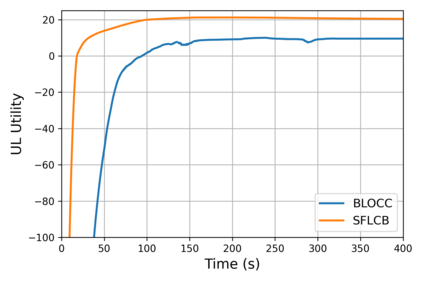
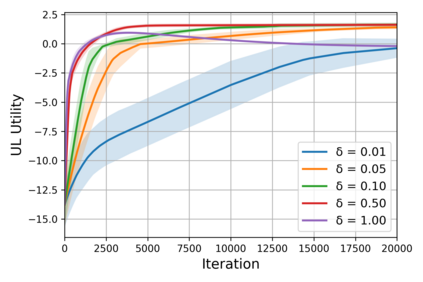
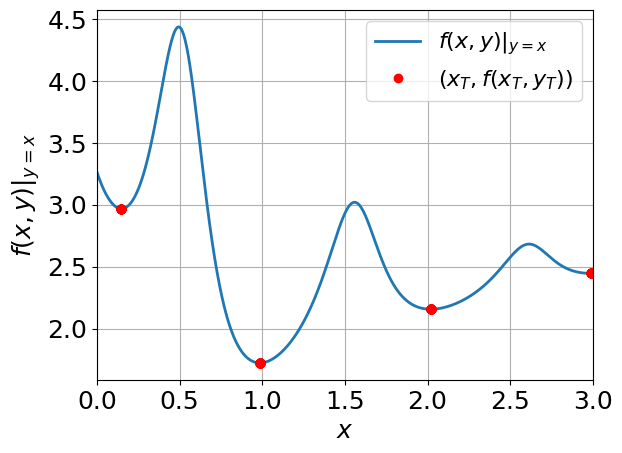
We study bilevel optimization problems where the lower-level problems are strongly convex and have coupled linear constraints. To overcome the potential non-smoothness of the hyper-objective and the computational challenges associated with the Hessian matrix, we utilize penalty and augmented Lagrangian methods to reformulate the original problem as a single-level one. Especially, we establish a strong theoretical connection between the reformulated function and the original hyper-objective by characterizing the closeness of their values and derivatives. Based on this reformulation, we propose a single-loop, first-order algorithm for linearly constrained bilevel optimization (SFLCB). We provide rigorous analyses of its non-asymptotic convergence rates, showing an improvement over prior double-loop algorithms -- form $O(\epsilon^{-3}\log(\epsilon^{-1}))$ to $O(\epsilon^{-3})$. The experiments corroborate our theoretical findings and demonstrate the practical efficiency of the proposed SFLCB algorithm. Simulation code is provided at https://github.com/ShenGroup/SFLCB.
翻译:暂无翻译