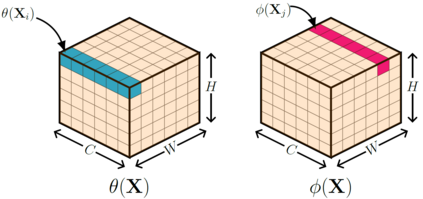
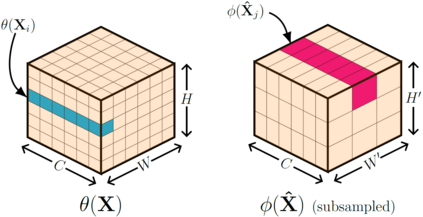
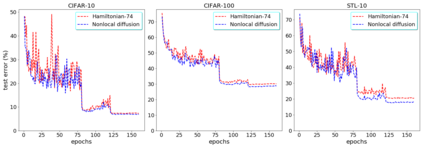
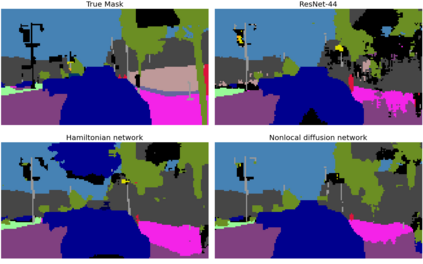
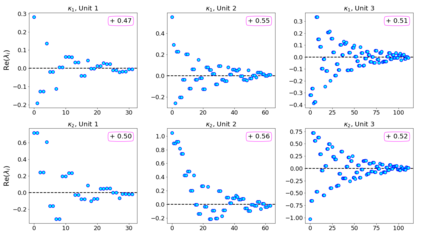
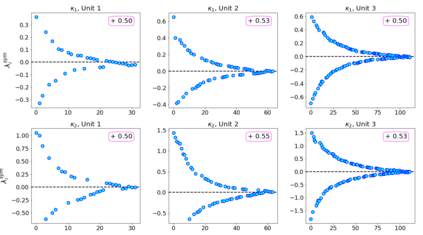
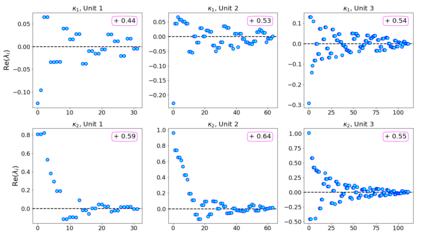
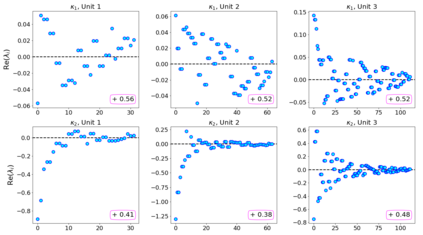
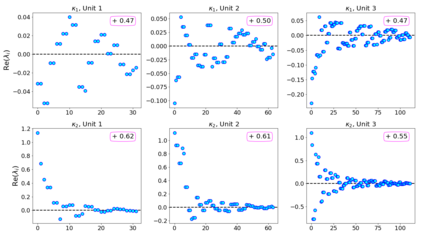
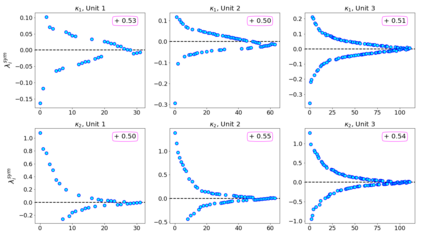
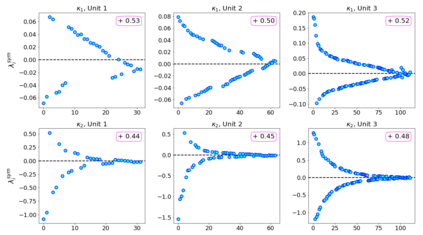
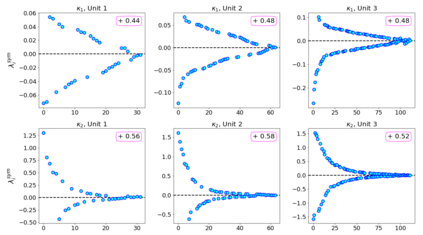
In this paper, we propose neural networks that tackle the problems of stability and field-of-view of a Convolutional Neural Network (CNN). As an alternative to increasing the network's depth or width to improve performance, we propose integral-based spatially nonlocal operators which are related to global weighted Laplacian, fractional Laplacian and inverse fractional Laplacian operators that arise in several problems in the physical sciences. The forward propagation of such networks is inspired by partial integro-differential equations (PIDEs). We test the effectiveness of the proposed neural architectures on benchmark image classification datasets and semantic segmentation tasks in autonomous driving. Moreover, we investigate the extra computational costs of these dense operators and the stability of forward propagation of the proposed neural networks.
翻译:在本文中,我们建议建立神经网络,以解决一个进化神经网络的稳定性和视野问题。作为提高网络深度或宽度以提高性能的替代办法,我们提议建立基于整体空间的非本地运营商,这些运营商涉及全球加权拉普拉西亚、分数拉普拉西亚和反向拉普拉西亚操作商,这些运营商在物理科学的若干问题中出现。这种网络的前沿传播受到局部内分化方程(PIDES)的启发。我们测试拟议的神经结构在基准图像分类数据集和自主驱动的语义分割任务方面的有效性。此外,我们调查这些密集运营商的额外计算成本和拟议神经网络的前沿传播的稳定性。