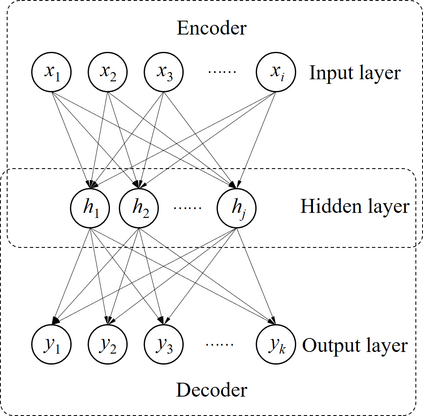
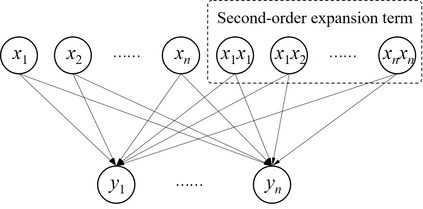
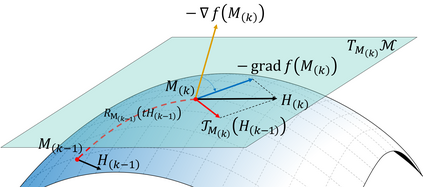
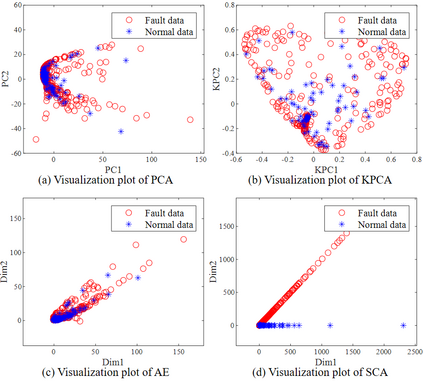
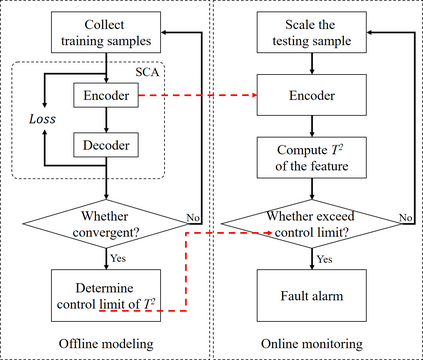
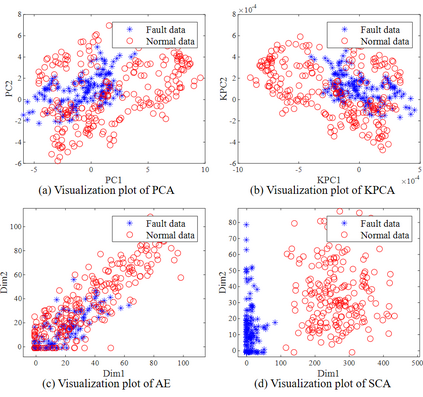
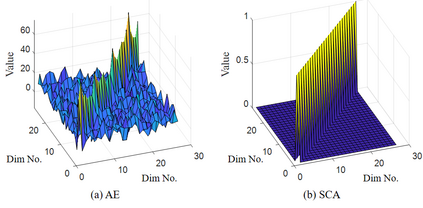
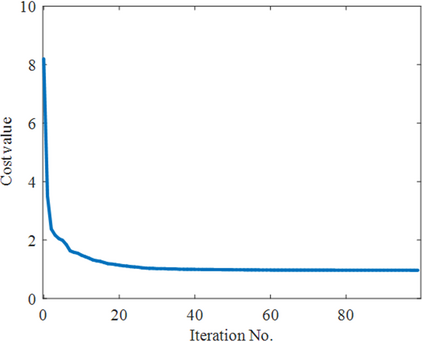
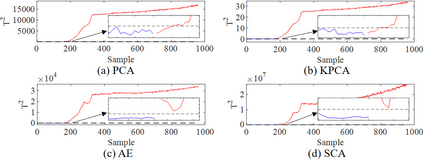
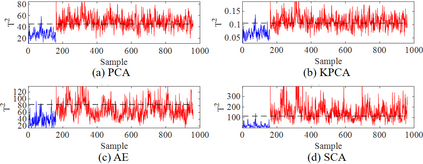
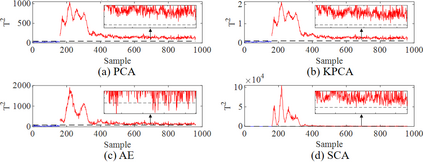
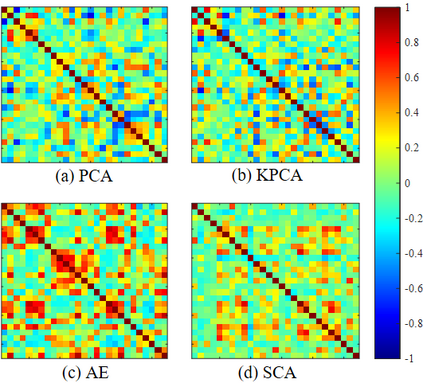
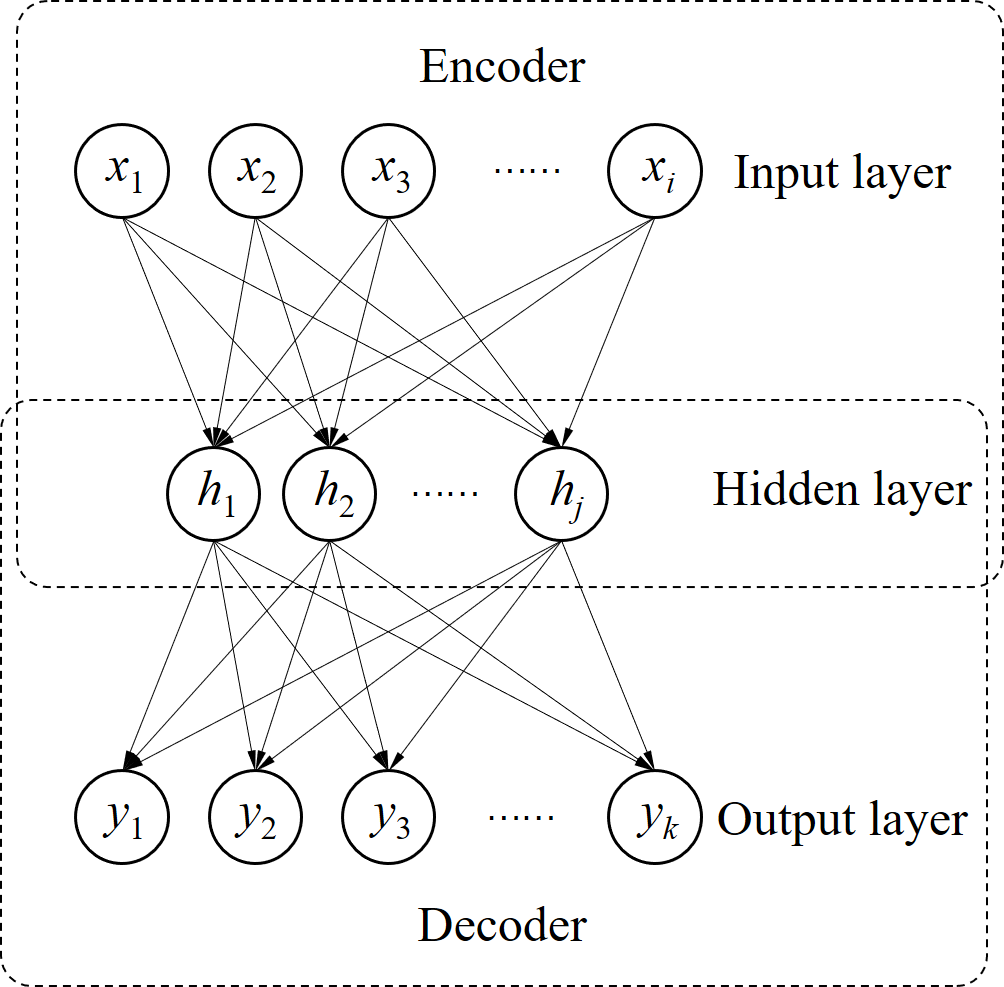
Process monitoring based on neural networks is getting more and more attention. Compared with classical neural networks, high-order neural networks have natural advantages in dealing with heteroscedastic data. However, high-order neural networks might bring the risk of overfitting and learning both the key information from original data and noises or anomalies. Orthogonal constraints can greatly reduce correlations between extracted features, thereby reducing the overfitting risk. This paper proposes a novel fault detection method called second-order component analysis (SCA). SCA rules out the heteroscedasticity of pro-cess data by optimizing a second-order autoencoder with orthogonal constraints. In order to deal with this constrained optimization problem, a geometric conjugate gradient algorithm is adopted in this paper, which performs geometric optimization on the combination of Stiefel manifold and Euclidean manifold. Extensive experiments on the Tennessee-Eastman benchmark pro-cess show that SCA outperforms PCA, KPCA, and autoencoder in missed detection rate (MDR) and false alarm rate (FAR).
翻译:基于神经网络的工艺监测越来越受到越来越多的关注。与古典神经网络相比,高阶神经网络在处理超度数据方面自然具有优势。然而,高阶神经网络可能会带来从原始数据和噪音或异常中过度匹配和学习关键信息的风险。正统限制可大大降低提取特性之间的关联,从而降低超度风险。本文件提出了一种新型的缺陷检测方法,称为二阶部件分析(SCA)。SCA通过优化二阶自动调节器来排除辅助系统数据的超度性。为了应对这一受限制的优化问题,本文采用了几何等同形梯度梯度算法,该算法对Stiefel多式和欧立底多式组合进行几何性优化。关于田纳西-东曼基准参数的大规模实验显示,SCA超越了五氯苯甲、KPA和失密检测率的自动编码(MDR)和假警报率(FAR)。