Linear slices of hyperbolic polynomials and positivity of symmetric polynomial functions

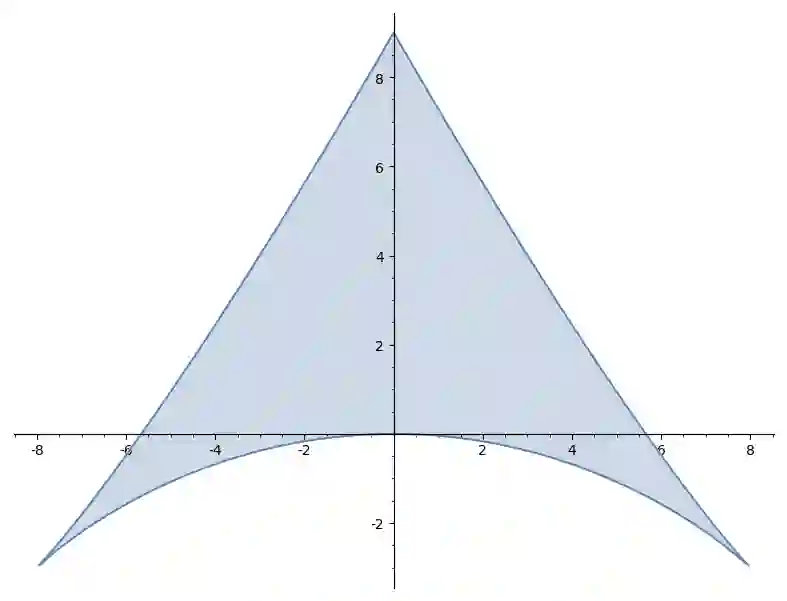
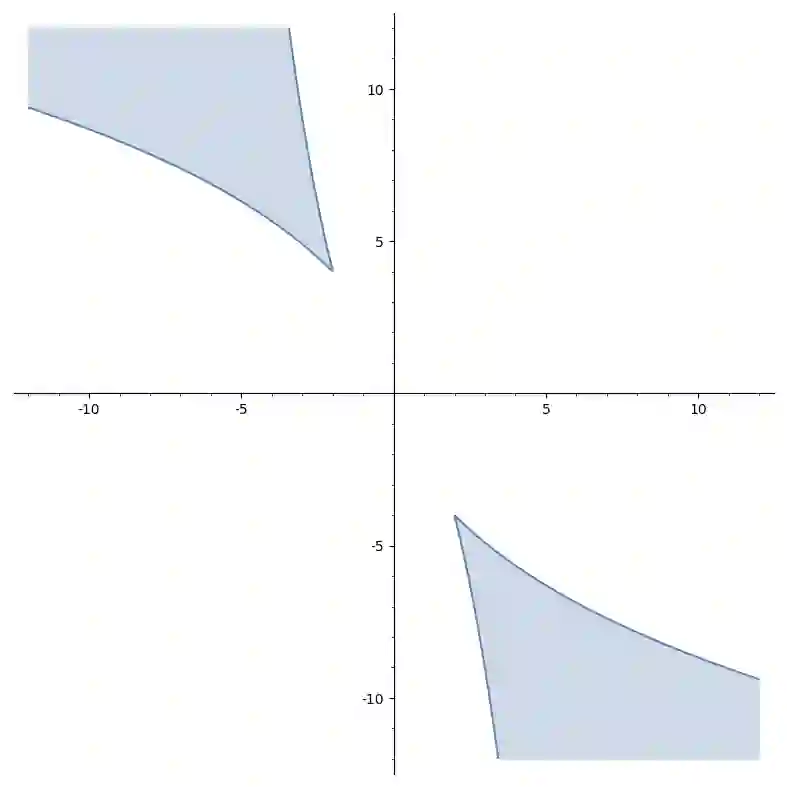
A real univariate polynomial of degree $n$ is called hyperbolic if all of its $n$ roots are on the real line. Such polynomials appear quite naturally in different applications, for example, in combinatorics and optimization. The focus of this article are families of hyperbolic polynomials which are determined through $k$ linear conditions on the coefficients. The coefficients corresponding to such a family of hyperbolic polynomials form a semi-algebraic set which we call a \emph{hyperbolic slice}. We initiate here the study of the geometry of these objects in more detail. The set of hyperbolic polynomials is naturally stratified with respect to the multiplicities of the real zeros and this stratification induces also a stratification on the hyperbolic slices. Our main focus here is on the \emph{local extreme points} of hyperbolic slices, i.e., the local extreme points of linear functionals, and we show that these correspond precisely to those hyperbolic polynomials in the hyperbolic slice which have at most $k$ distinct roots and we can show that generically the convex hull of such a family is a polyhedron. Building on these results, we give consequences of our results to the study of symmetric real varieties and symmetric semi-algebraic sets. Here, we show that sets defined by symmetric polynomials which can be expressed sparsely in terms of elementary symmetric polynomials can be sampled on points with few distinct coordinates. This in turn allows for algorithmic simplifications, for example, to verify that such polynomials are non-negative or that a semi-algebraic set defined by such polynomials is empty.