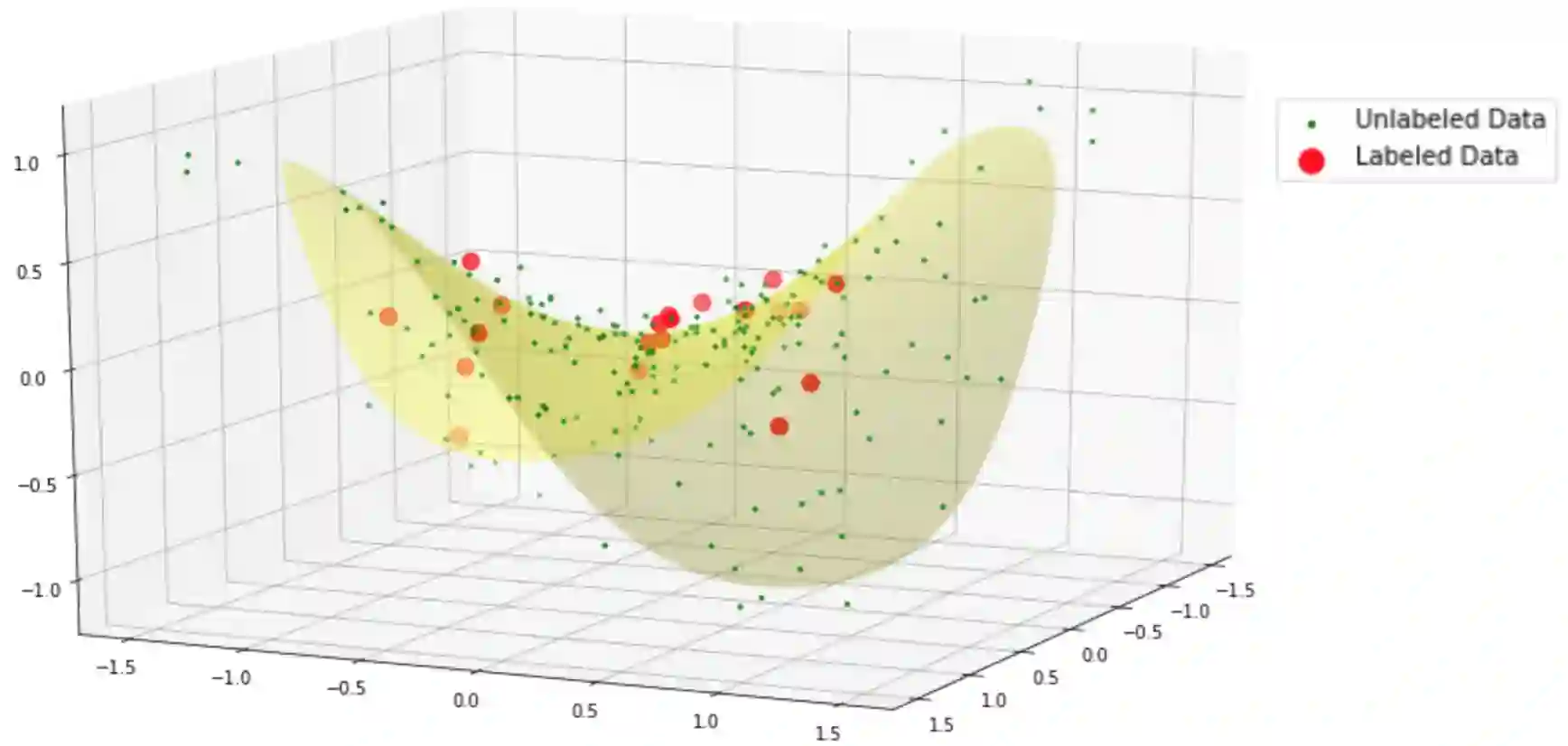
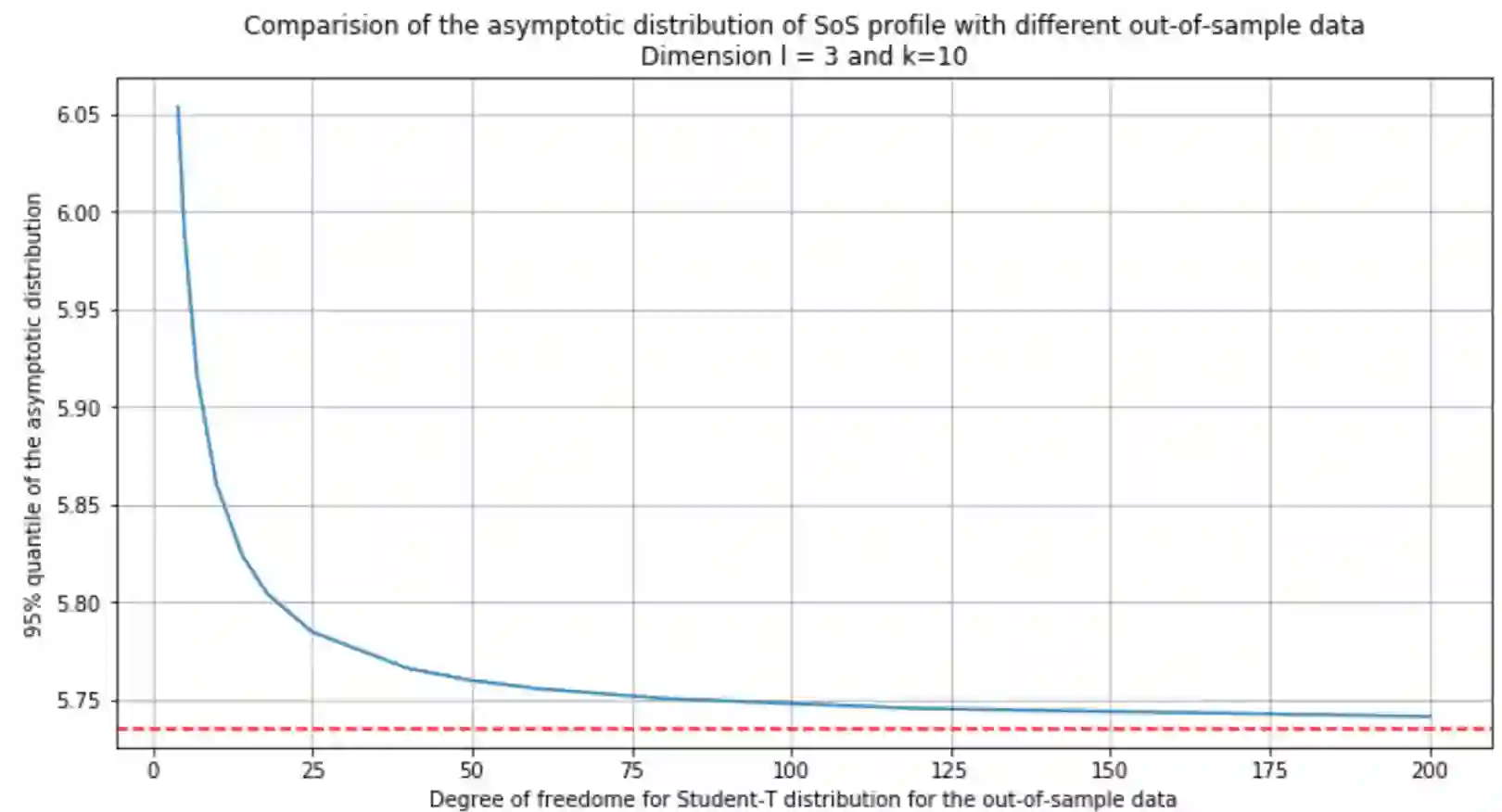
We present a novel inference approach that we call Sample Out-of-Sample (or SOS) inference. The approach can be used widely, ranging from semi-supervised learning to stress testing, and it is fundamental in the application of data-driven Distributionally Robust Optimization (DRO). Our method enables measuring the impact of plausible out-of-sample scenarios in a given performance measure of interest, such as a financial loss. The methodology is inspired by Empirical Likelihood (EL), but we optimize the empirical Wasserstein distance (instead of the empirical likelihood) induced by observations. From a methodological standpoint, our analysis of the asymptotic behavior of the induced Wasserstein-distance profile function shows dramatic qualitative differences relative to EL. For instance, in contrast to EL, which typically yields chi-squared weak convergence limits, our asymptotic distributions are often not chi-squared. Also, the rates of convergence that we obtain have some dependence on the dimension in a non-trivial way but remain controlled as the dimension increases.
翻译:我们提出了一个新型的推论方法,我们称之为“抽样出抽样(SOS)推论 ” 。 这种方法可以广泛使用,从半监督的学习到压力测试,在应用数据驱动的分布式优化优化优化(DRO)中具有根本意义。 我们的方法可以测量在某种利益绩效衡量(如财政损失)中可能存在的出抽样情景的影响。 这种方法受“ 经验相似性( EL) ” 的启发, 但我们优化了观测产生的经验性瓦瑟斯坦距离(而不是经验可能性 ) 。 从方法角度看,我们对引致的瓦瑟尔-远距谱功能的无症状行为的分析显示了与EL(DRO)相比在质量上的巨大差异。 例如,与EL(通常产生奇异的聚合弱点)相比, 我们的亚麻药分布往往不相近。 另外,我们获得的趋同率在一定程度上依赖非三维维维的维度,但随着维度的增加而继续受到控制。