Nonlinear material identification of heterogeneous isogeometric Kirchhoff-Love shells

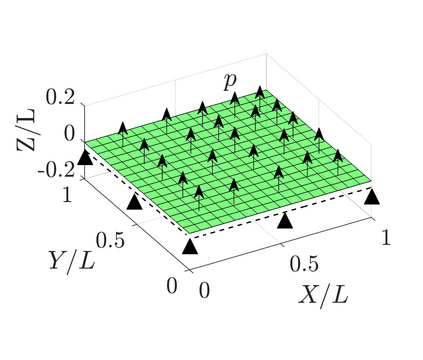
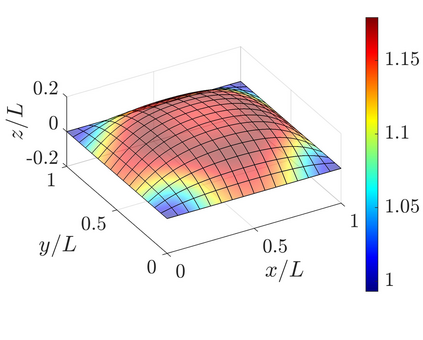
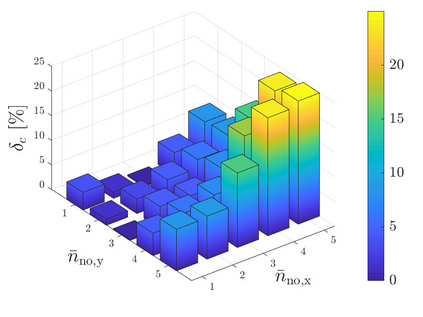
This work presents a Finite Element Model Updating inverse methodology for reconstructing heterogeneous material distributions based on an efficient isogeometric shell formulation. It uses a nonlinear material model with a hyperelastic incompressible Neo-Hookean membrane part and a Canham bending part. The material distribution is discretized by linear elements such that the nodal values are the design variables to be identified. Independent FE and material discretization, as well as flexible incorporation of experimental data, offer high robustness and control. Three elementary test cases, which exhibit large deformations and different challenges, are considered: uniaxial tension, pure bending, and sheet inflation. Experiment-like results are generated from high-resolution simulations with the subsequent addition of up to 4% noise. Local optimization based on the trust-region approach is used. The results show that with a sufficient amount of experimental measurements, the algorithm is capable to reconstruct material distributions with high precision even in the presence of large noise. The proposed formulation is very general, facilitating its extension to other material models and optimization algorithms. For the latter, the analytically derived sensitivities are provided.