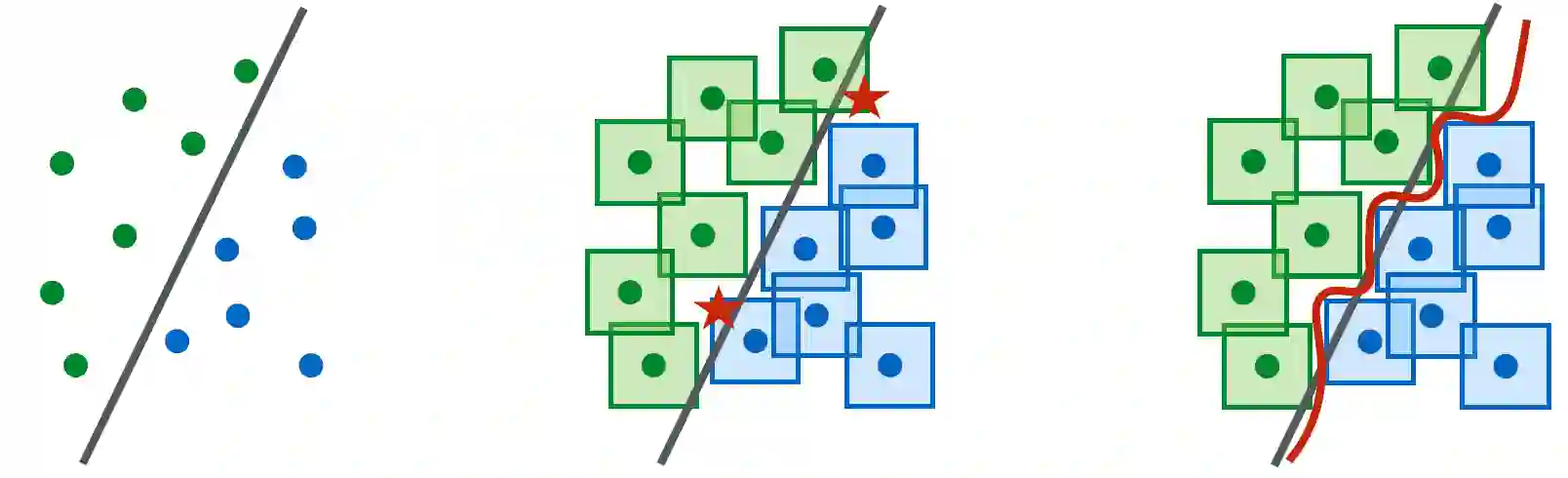
We establish an equivalence between a family of adversarial training problems for non-parametric binary classification and a family of regularized risk minimization problems where the regularizer is a nonlocal perimeter functional. The resulting regularized risk minimization problems admit exact convex relaxations of the type $L^1+$ (nonlocal) $\operatorname{TV}$, a form frequently studied in image analysis and graph-based learning. A rich geometric structure is revealed by this reformulation which in turn allows us to establish a series of properties of optimal solutions of the original problem, including the existence of minimal and maximal solutions (interpreted in a suitable sense), and the existence of regular solutions (also interpreted in a suitable sense). In addition, we highlight how the connection between adversarial training and perimeter minimization problems provides a novel, directly interpretable, statistical motivation for a family of regularized risk minimization problems involving perimeter/total variation. The majority of our theoretical results are independent of the distance used to define adversarial attacks.
翻译:在非参数二进制分类和正规化风险最小化问题(正规化器是非局部的外围功能)之间,我们建立了对等的对立培训问题家庭与正规化风险最小化问题家庭之间的等同,由此产生的对立风险最小化问题承认了美元1+美元(非本地)美元(operatorname{TV}$)这一在图像分析和基于图表的学习中经常研究的一种形式,这一重整揭示了丰富的几何结构,从而使我们能够确定一系列最佳解决原始问题的办法,包括存在最低限度和最高程度的解决方案(适当解释),以及存在定期解决方案(也适当解释)。此外,我们强调敌对式培训与外围最小化问题之间的联系如何为那些面临正规化风险最小化问题的家庭提供了新的、可直接解释的统计动机,涉及周边/整体变异性。我们的理论结果大多与用来界定对抗性攻击的距离无关。