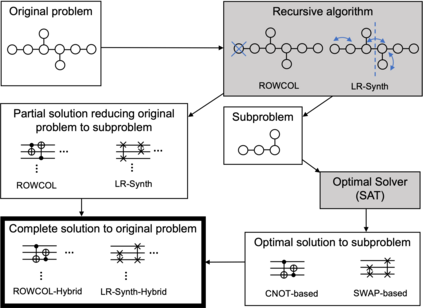
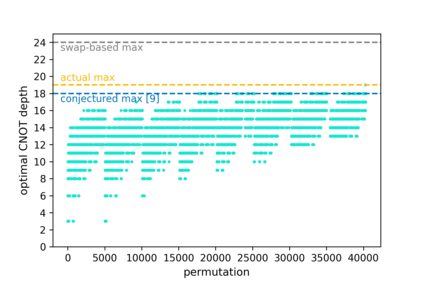
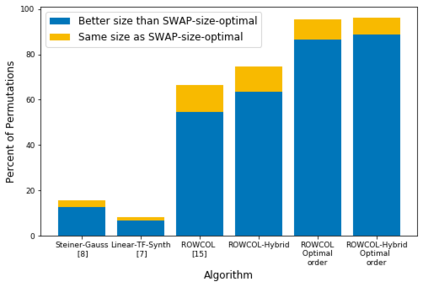
We describe a family of recursive methods for the synthesis of qubit permutations on quantum computers with limited qubit connectivity. Two objectives are of importance: circuit size and depth. In each case we combine a scalable heuristic with a non-scalable, yet exact, synthesis. Our algorithms are applicable to generic connectivity constraints, scale favorably, and achieve close-to-optimal performance in many cases. We demonstrate the utility of these algorithms by optimizing the compilation of Quantum Volume circuits, and to disprove an old conjecture on reversals being the hardest permutation on a path.
翻译:我们描述的是一组循环方法,用于合成量子计算机中连接有限量子的qubit变异。有两个目标很重要:电路大小和深度。在每一种情况下,我们把可伸缩的螺旋体与不可伸缩的、但准确的合成结合起来。我们的算法适用于通用连通限制,在很多情况下,规模优异,并实现近于最佳的性能。我们通过优化量子量子量子电路的汇编来展示这些算法的效用,并反驳关于逆向是一条道路上最难变的老的预测。