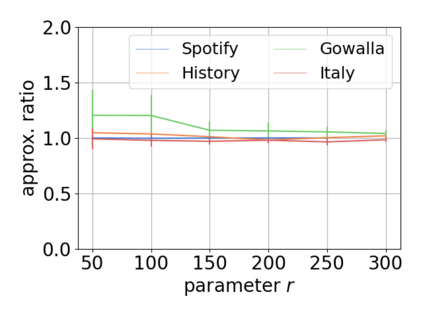
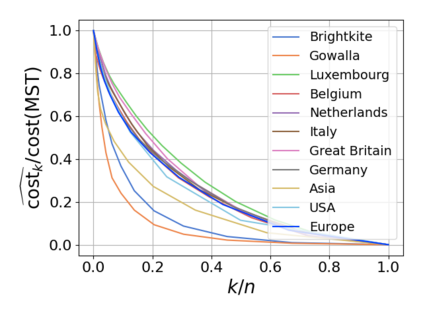
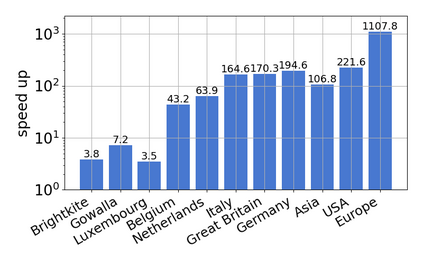
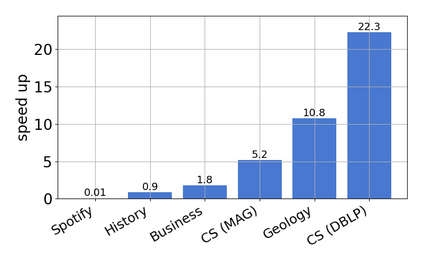
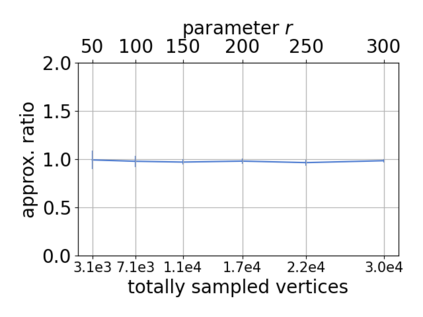
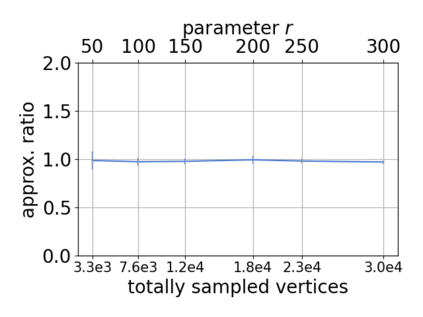
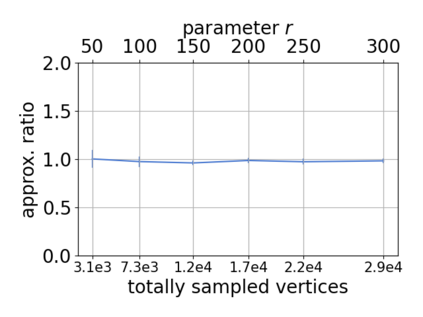
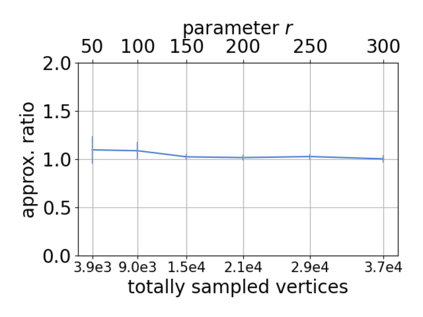
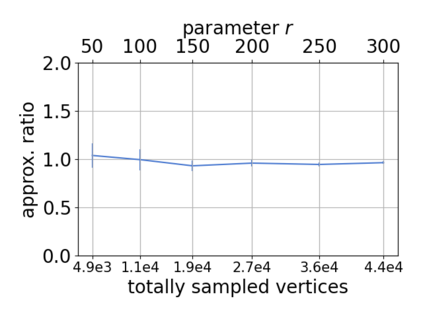
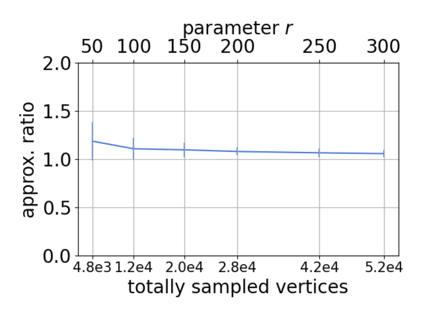
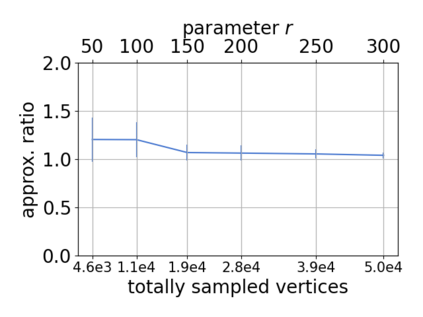
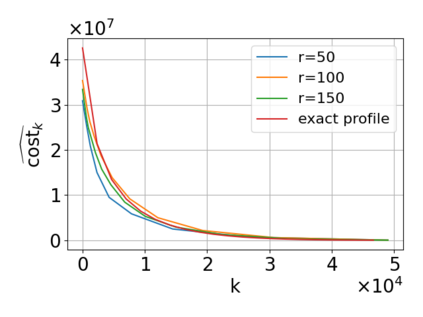
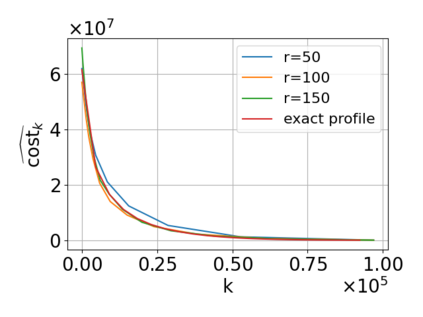
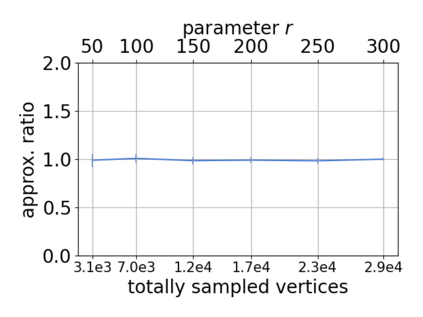
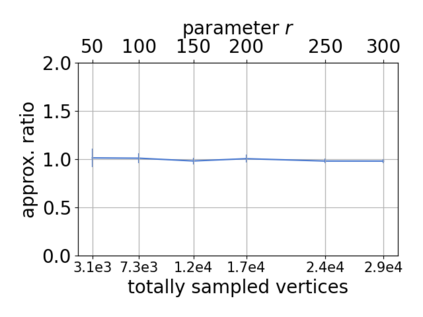
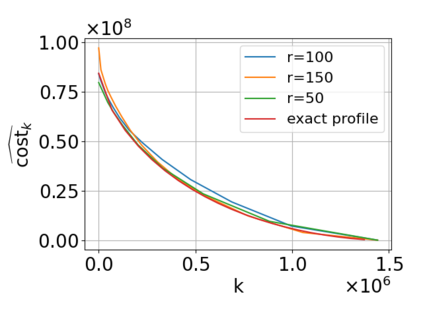
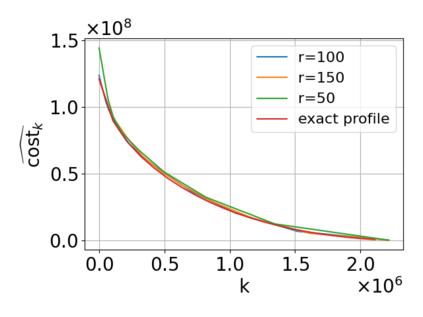
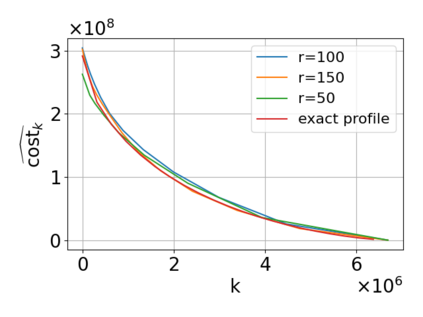
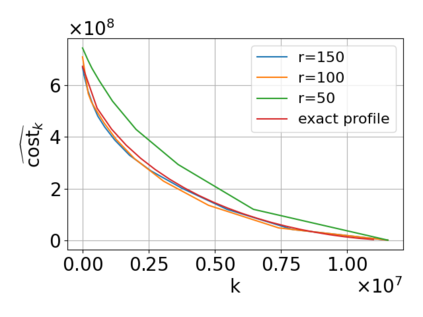
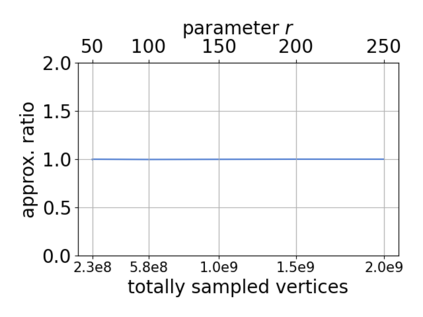
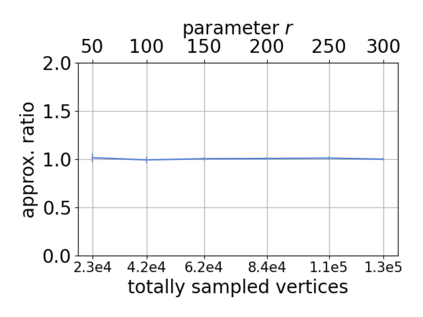
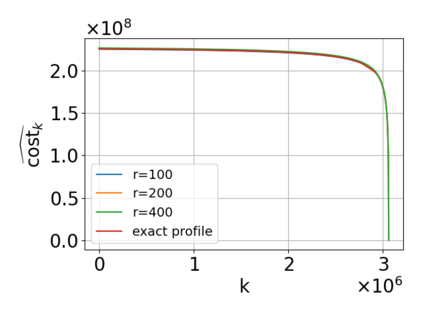
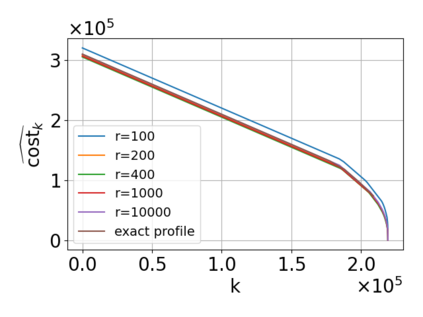
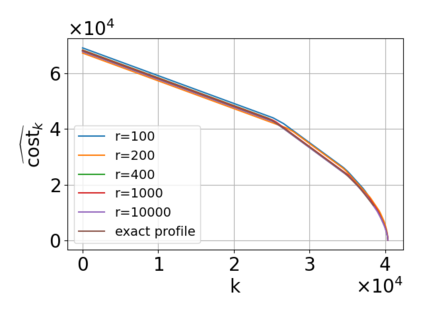
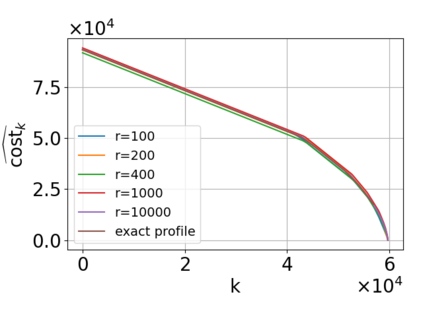
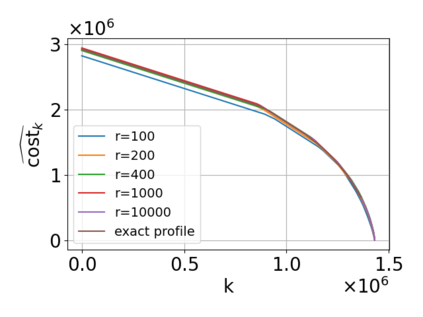
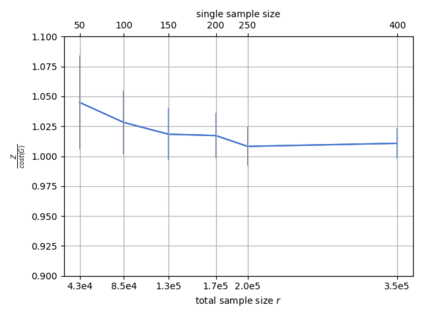
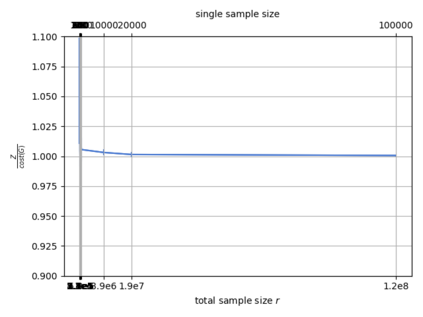
Single-linkage clustering is a fundamental method for data analysis. Algorithmically, one can compute a single-linkage $k$-clustering (a partition into $k$ clusters) by computing a minimum spanning tree and dropping the $k-1$ most costly edges. This clustering minimizes the sum of spanning tree weights of the clusters. This motivates us to define the cost of a single-linkage $k$-clustering as the weight of the corresponding spanning forest, denoted by $\mathrm{cost}_k$. Besides, if we consider single-linkage clustering as computing a hierarchy of clusterings, the total cost of the hierarchy is defined as the sum of the individual clusterings, denoted by $\mathrm{cost}(G) = \sum_{k=1}^{n} \mathrm{cost}_k$. In this paper, we assume that the distances between data points are given as a graph $G$ with average degree $d$ and edge weights from $\{1,\dots, W\}$. Given query access to the adjacency list of $G$, we present a sampling-based algorithm that computes a succinct representation of estimates $\widehat{\mathrm{cost}}_k$ for all $k$. The running time is $\tilde O(d\sqrt{W}/\varepsilon^3)$, and the estimates satisfy $\sum_{k=1}^{n} |\widehat{\mathrm{cost}}_k - \mathrm{cost}_k| \le \varepsilon\cdot \mathrm{cost}(G)$, for any $0<\varepsilon <1$. Thus we can approximate the cost of every $k$-clustering upto $(1+\varepsilon)$ factor \emph{on average}. In particular, our result ensures that we can estimate $\cost(G)$ upto a factor of $1\pm \varepsilon$ in the same running time. We also extend our results to the setting where edges represent similarities. In this case, the clusterings are defined by a maximum spanning tree, and our algorithms run in $\tilde{O}(dW/\varepsilon^3)$ time. We futher prove nearly matching lower bounds for estimating the total clustering cost and we extend our algorithms to metric space settings.
翻译:暂无翻译