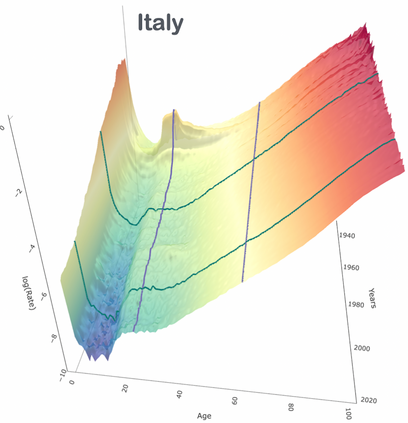
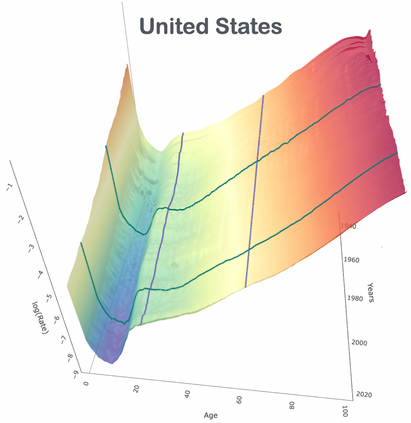
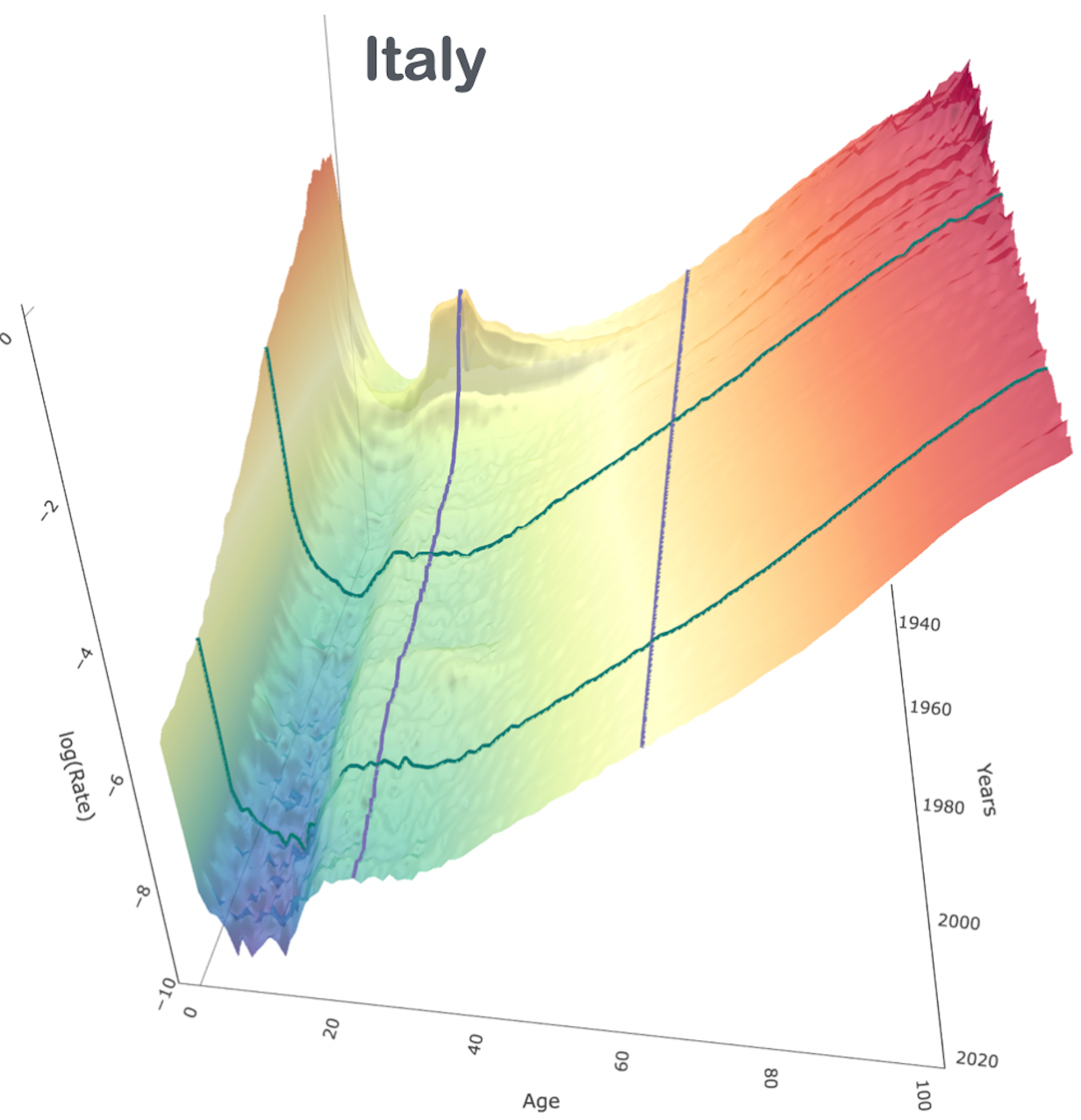
Although the analysis of human mortality has a well-established history, the attempt to accurately forecast future death-rate patterns for different age groups and time horizons still attracts active research. Such a predictive focus has motivated an increasing shift towards more flexible representations of age-specific period mortality trajectories at the cost of reduced interpretability. Although this perspective has led to successful predictive strategies, the inclusion of interpretable structures in modeling of human mortality can be, in fact, beneficial for improving forecasts. We pursue this direction via a novel B-spline process with locally-adaptive dynamic coefficients. Such a process outperforms state-of-the-art forecasting strategies by explicitly incorporating the core structures of period mortality within an interpretable formulation which enables inference on age-specific mortality trends and the corresponding rates of change across time. This is obtained by modeling the age-specific death counts via a Poisson log-normal model parameterized through a linear combination of B-spline bases with dynamic coefficients that characterize time changes in mortality rates via suitable stochastic differential equations. While flexible, the resulting formulation can be accurately approximated by a Gaussian state-space model that facilitates closed-form Kalman filtering, smoothing and forecasting, for both the trends of the spline coefficients and the corresponding first derivatives, which measure rates of change in mortality for different ages. As illustrated in applications to mortality data from different countries, our model outperforms state-of-the-art methods both in point forecasts and in calibration of predictive intervals. Moreover, it unveils substantial differences in mortality patterns across countries and ages, both in the past decades and during the COVID-19 pandemic.
翻译:暂无翻译