Move Schedules: Fast persistence computations in coarse dynamic settings

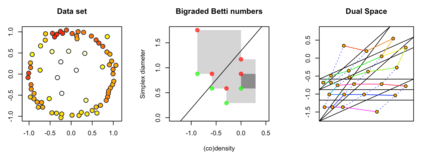
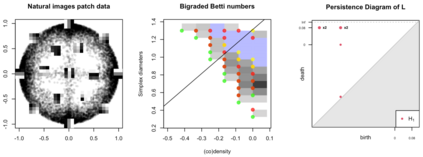
The standard procedure for computing the persistent homology of a filtered simplicial complex is the matrix reduction algorithm. Its output is a particular decomposition of the total boundary matrix, from which the persistence diagrams and generating cycles can be derived. Persistence diagrams are known to vary continuously with respect to their input, which motivates the algorithmic study of persistence computations for time-varying filtered complexes. Computationally, simulating persistence dynamically can be reduced to maintaining a valid decomposition under adjacent transpositions in the filtration order. In practice, the quadratic scaling in the number of such transpositions often makes this maintenance procedure slower than simply computing the decomposition from scratch, limiting the application of dynamic persistence to relatively small data sets. In this work, we propose a coarser strategy for maintaining the decomposition over a 1-parameter family of filtrations. Our first result is an analysis of a simple linear-time strategy which reduces the number of column operations needed to simulate persistence across a fixed homotopy by at most a factor of 2. We show a modification of this technique which maintains only a sublinear number of valid states, as opposed to a quadratic number of states, and we provide tight lower bounds for this technique. Finally, we present results showing that the decrease in operations to compute diagrams across a family of filtrations is proportional to the difference between the expected quadratic number of states, and the proposed sublinear coarsening. Applications to multi-dimensional persistence and crocker stacks are also presented.