Dynamic Ranking with the BTL Model: A Nearest Neighbor based Rank Centrality Method

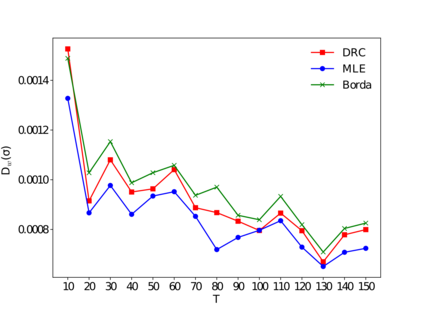
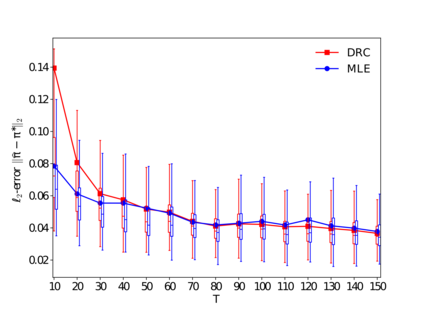
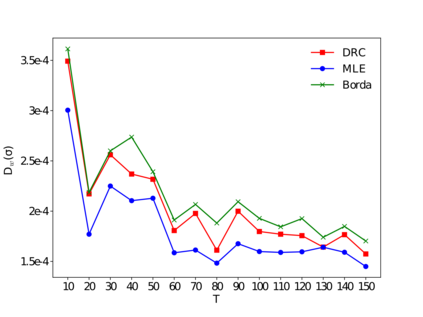
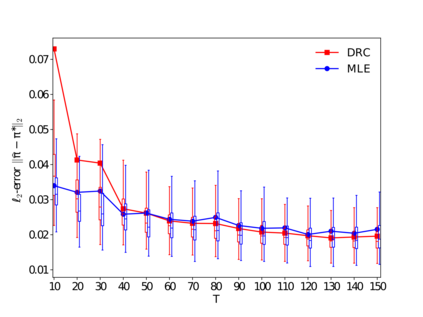
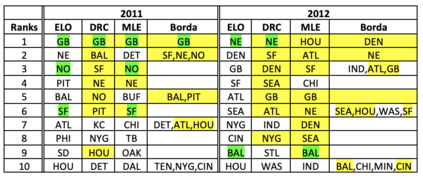
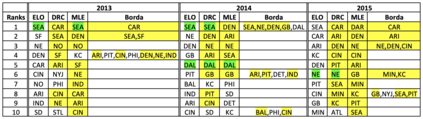
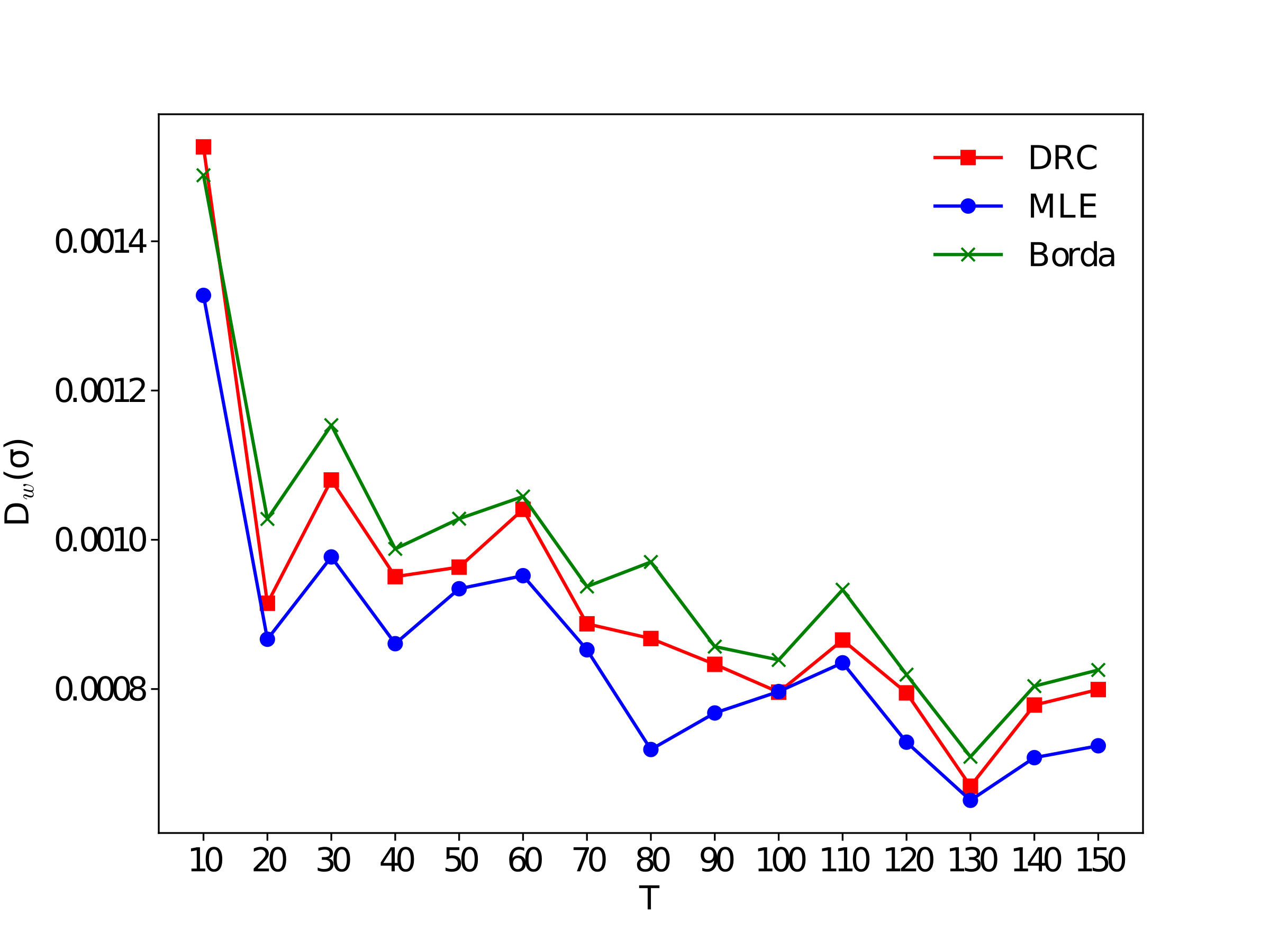
Many applications such as recommendation systems or sports tournaments involve pairwise comparisons within a collection of $n$ items, the goal being to aggregate the binary outcomes of the comparisons in order to recover the latent strength and/or global ranking of the items. In recent years, this problem has received significant interest from a theoretical perspective with a number of methods being proposed, along with associated statistical guarantees under the assumption of a suitable generative model. While these results typically collect the pairwise comparisons as one comparison graph $G$, however in many applications - such as the outcomes of soccer matches during a tournament - the nature of pairwise outcomes can evolve with time. Theoretical results for such a dynamic setting are relatively limited compared to the aforementioned static setting. We study in this paper an extension of the classic BTL (Bradley-Terry-Luce) model for the static setting to our dynamic setup under the assumption that the probabilities of the pairwise outcomes evolve smoothly over the time domain $[0,1]$. Given a sequence of comparison graphs $(G_{t'})_{t' \in \mathcal{T}}$ on a regular grid $\mathcal{T} \subset [0,1]$, we aim at recovering the latent strengths of the items $w_t \in \mathbb{R}^n$ at any time $t \in [0,1]$. To this end, we adapt the Rank Centrality method - a popular spectral approach for ranking in the static case - by locally averaging the available data on a suitable neighborhood of $t$. When $(G_{t'})_{t' \in \mathcal{T}}$ is a sequence of Erd\"os-Renyi graphs, we provide non-asymptotic $\ell_2$ and $\ell_{\infty}$ error bounds for estimating $w_t^*$ which in particular establishes the consistency of this method in terms of $n$, and the grid size $\lvert\mathcal{T}\rvert$. We also complement our theoretical analysis with experiments on real and synthetic data.