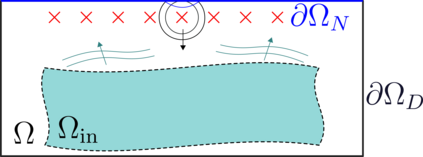
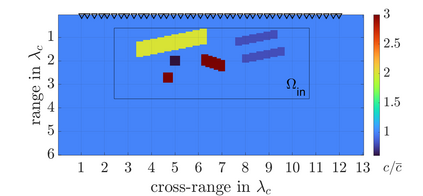
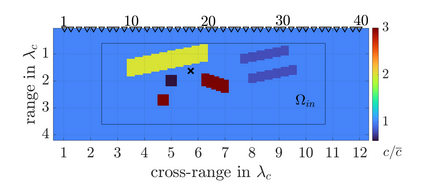
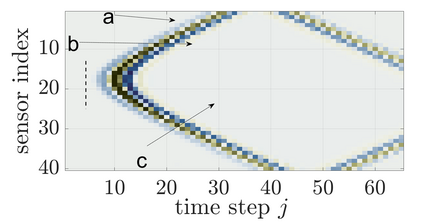
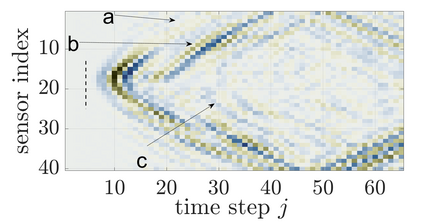
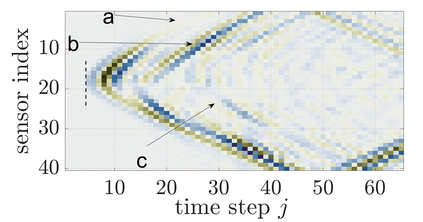
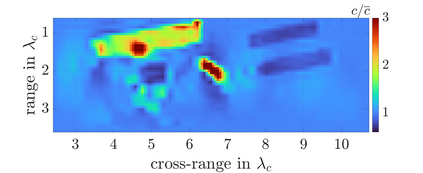
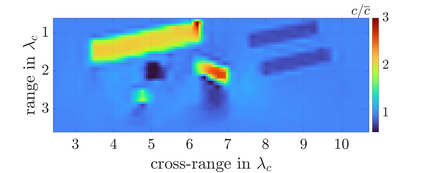
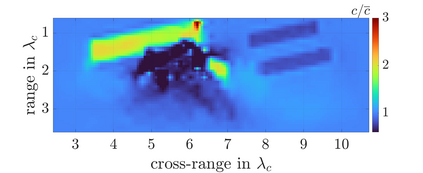
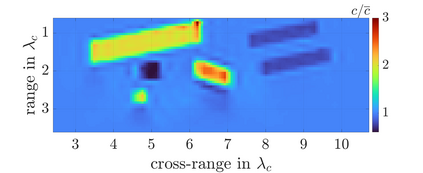
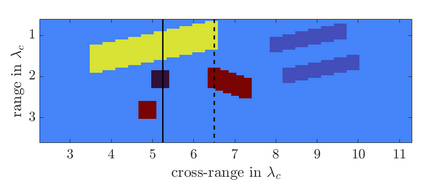
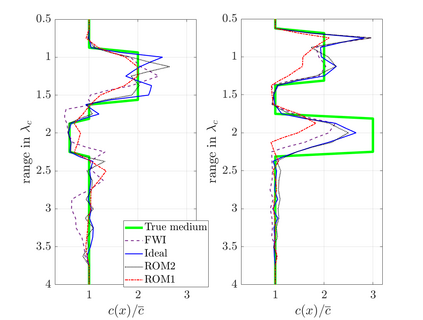
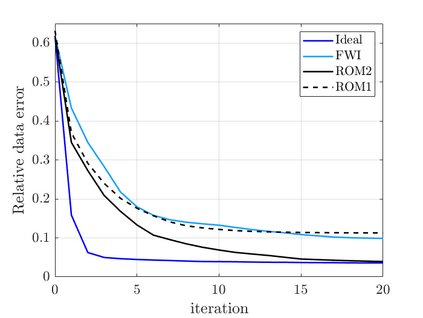
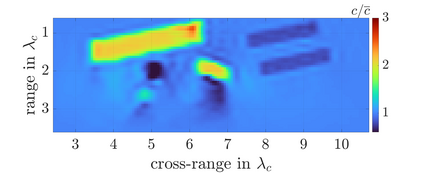
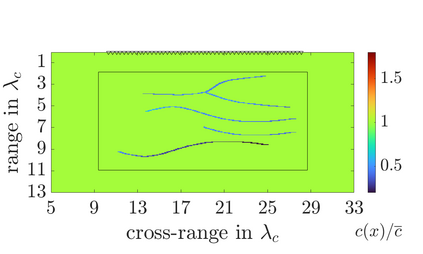
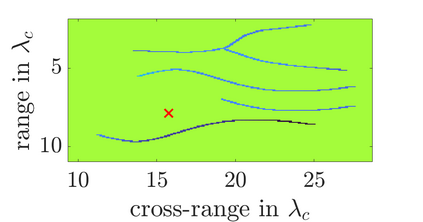
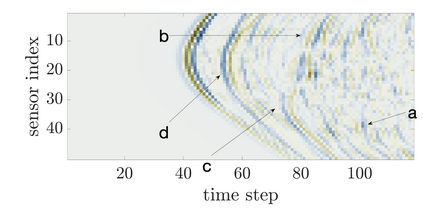
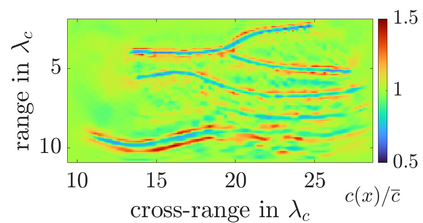
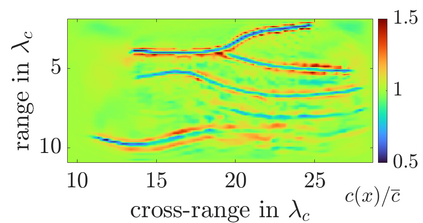
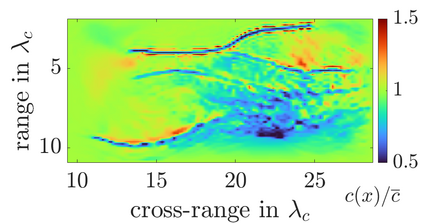
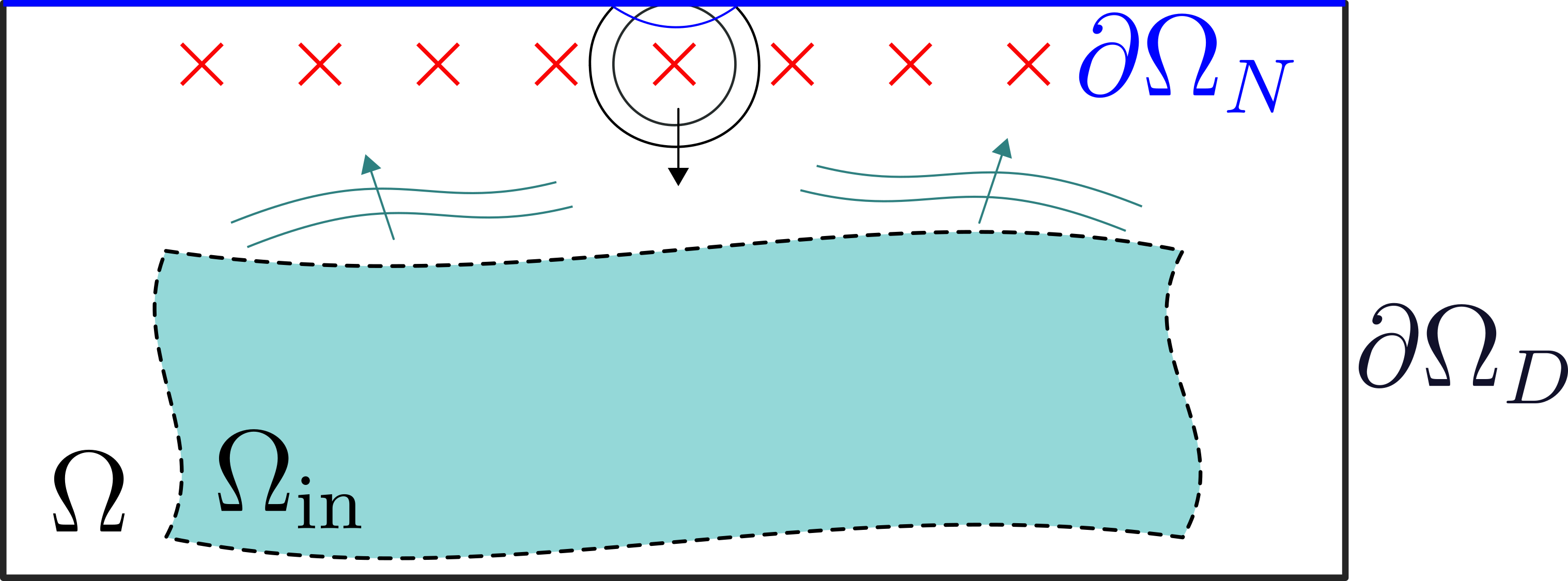
We study an inverse problem for the wave equation, concerned with estimating the wave speed, aka velocity, from data gathered by an array of sources and receivers that emit probing signals and measure the resulting waves. The typical mathematical formulation of velocity estimation is a nonlinear least squares minimization of the data misfit, over a search velocity space. There are two main impediments to this approach, which manifest as multiple local minima of the objective function: The nonlinearity of the mapping from the velocity to the data, which accounts for multiple scattering effects, and poor knowledge of the kinematics (smooth part of the wave speed) which causes cycle-skipping. We show that the nonlinearity can be mitigated using a data driven estimate of the internal wave field. This leads to improved performance of the inversion for a reasonable initial guess of the kinematics.
翻译:我们研究了波方程的一个反向问题,即从一系列来源和接收器收集的数据中估计波速、 aka速度,这些数据释放出探测信号并测量产生的波浪。速度估计的典型数学公式是,在搜索速度空间上,将数据误差减少到非线性最低方形最小。这种方法有两个主要障碍,表现为目标功能的多重局部微型:从速度到数据绘图的不线性性,数据是多种散射效应的计算因素,对引起周期滑动的动因学(波速的毛部部分)知之甚少。我们表明,通过以数据驱动的对内部波场的估计,非线性能是可以减轻的。这导致对运动场进行合理的初步猜测的改变性能得到改善。