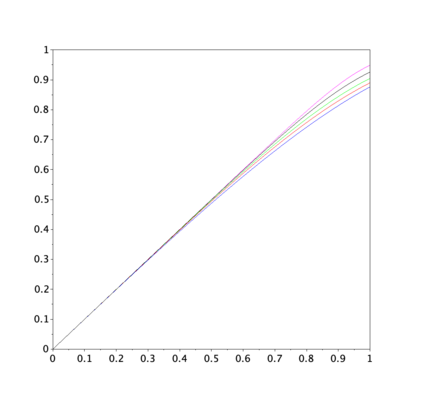
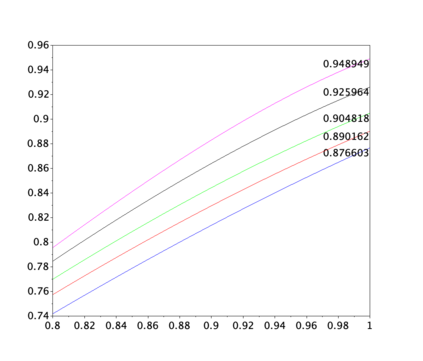
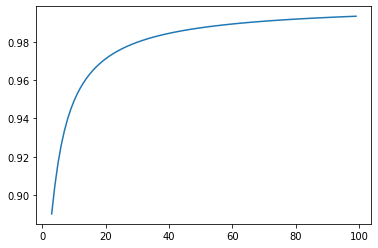
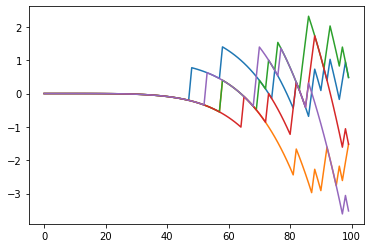
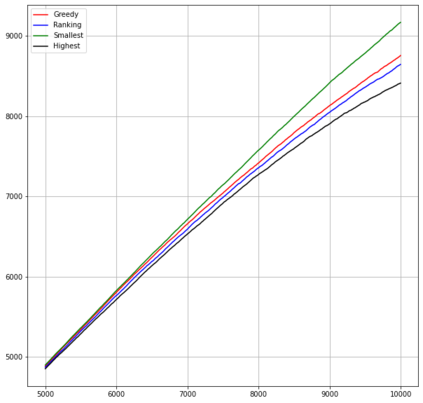
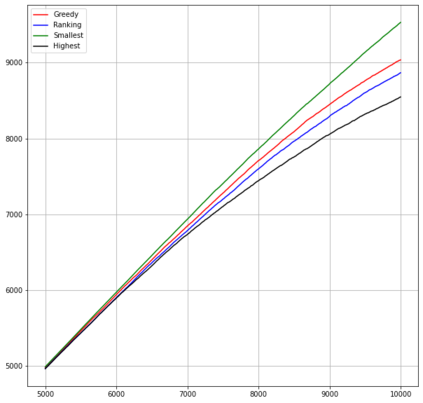
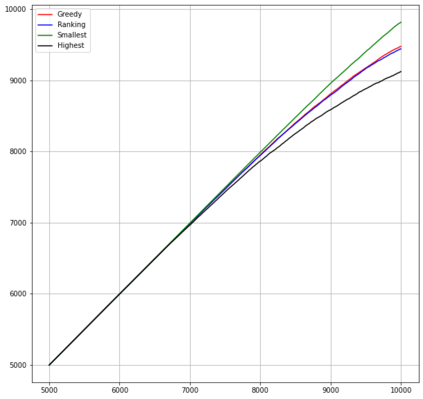
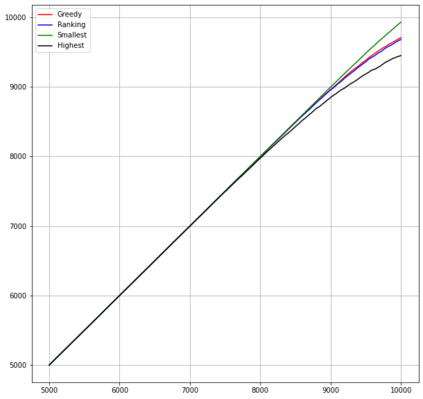
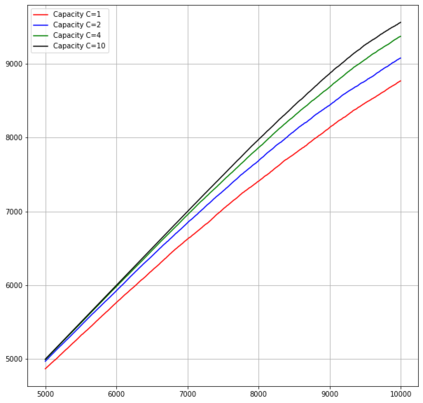
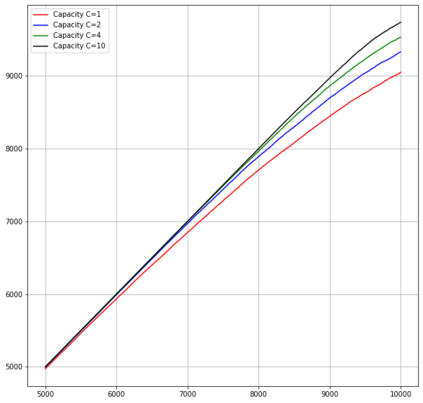
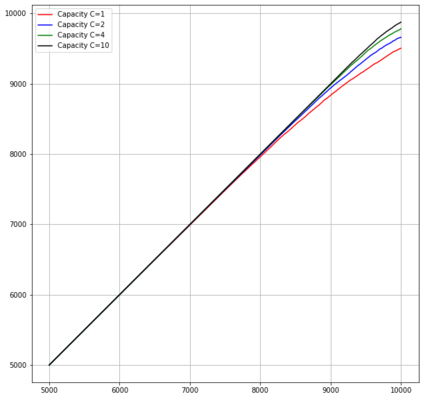
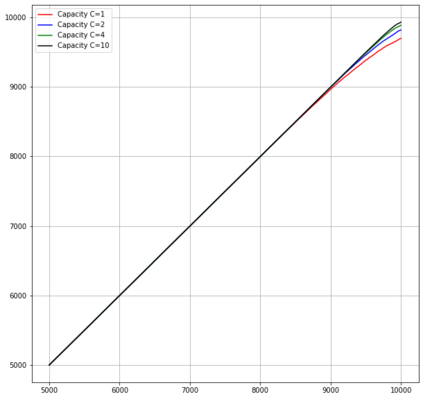
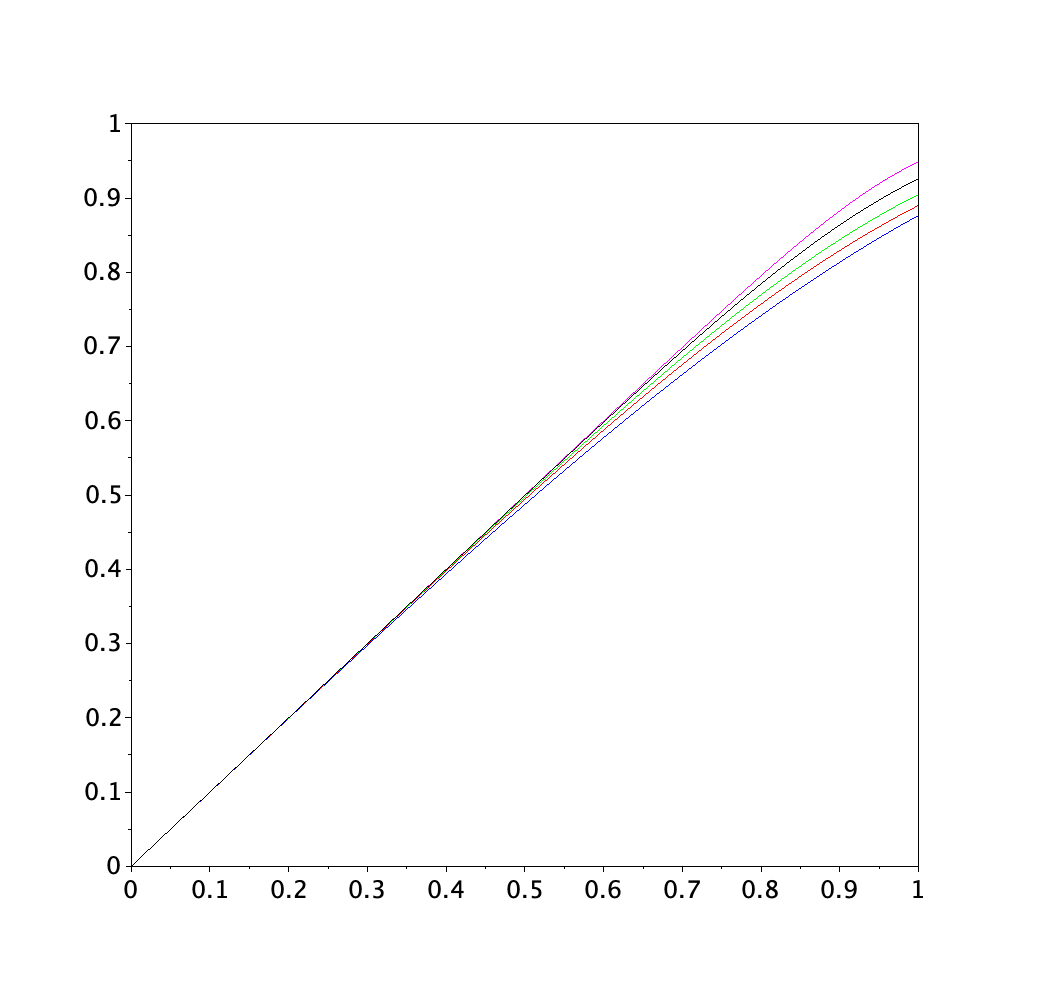
Motivated by sequential budgeted allocation problems, we investigate online matching problems where connections between vertices are not i.i.d., but they have fixed degree distributions -- the so-called configuration model. We estimate the competitive ratio of the simplest algorithm, GREEDY, by approximating some relevant stochastic discrete processes by their continuous counterparts, that are solutions of an explicit system of partial differential equations. This technique gives precise bounds on the estimation errors, with arbitrarily high probability as the problem size increases. In particular, it allows the formal comparison between different configuration models. We also prove that, quite surprisingly, GREEDY can have better performance guarantees than RANKING, another celebrated algorithm for online matching that usually outperforms the former.
翻译:基于按顺序编制预算的分配问题,我们调查在线匹配问题,因为脊椎之间联系不是i.d.d.,但有固定的度分布 -- -- 所谓的配置模型。我们估计最简单的算法GREEDY的竞争性比重,即GREEDY,通过连续对口方的近似一些相关随机离散过程,这些过程是局部差异方程的明确系统的解决办法。这种技术为估计错误提供了精确的界限,随着问题规模的增加,这种估计误差的概率任意很高。特别是,它允许对不同的配置模型进行正式比较。我们还证明,非常令人惊讶的是,GREEDY的性能保障比RANKING(另一个著名的在线匹配算法,通常优于前者的)要好得多。