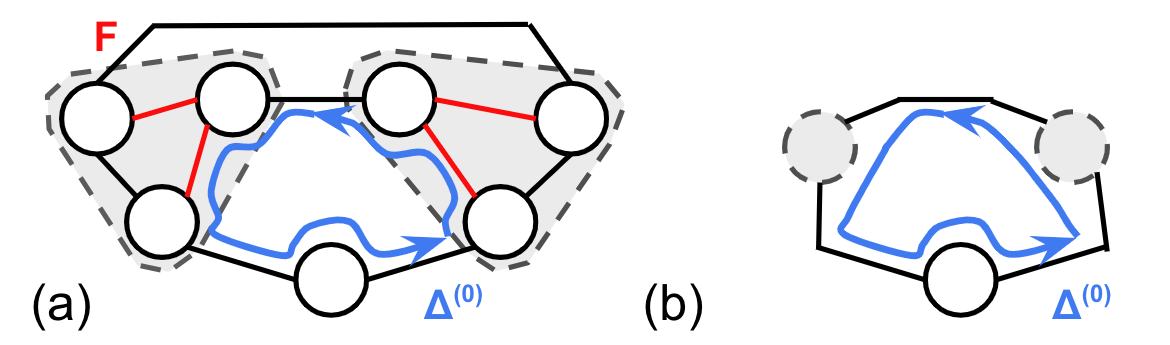
We give a deterministic $m^{1+o(1)}$ time algorithm that computes exact maximum flows and minimum-cost flows on directed graphs with $m$ edges and polynomially bounded integral demands, costs, and capacities. As a consequence, we obtain the first running time improvement for deterministic algorithms that compute maximum-flow in graphs with polynomial bounded capacities since the work of Goldberg-Rao [J.ACM '98]. Our algorithm builds on the framework of Chen-Kyng-Liu-Peng-Gutenberg-Sachdeva [FOCS '22] that computes an optimal flow by computing a sequence of $m^{1+o(1)}$-approximate undirected minimum-ratio cycles. We develop a deterministic dynamic graph data-structure to compute such a sequence of minimum-ratio cycles in an amortized $m^{o(1)}$ time per edge update. Our key technical contributions are deterministic analogues of the vertex sparsification and edge sparsification components of the data-structure from Chen et al. For the vertex sparsification component, we give a method to avoid the randomness in Chen et al. which involved sampling random trees to recurse on. For the edge sparsification component, we design a deterministic algorithm that maintains an embedding of a dynamic graph into a sparse spanner. We also show how our dynamic spanner can be applied to give a deterministic data structure that maintains a fully dynamic low-stretch spanning tree on graphs with polynomially bounded edge lengths, with subpolynomial average stretch and subpolynomial amortized time per edge update.
翻译:暂无翻译