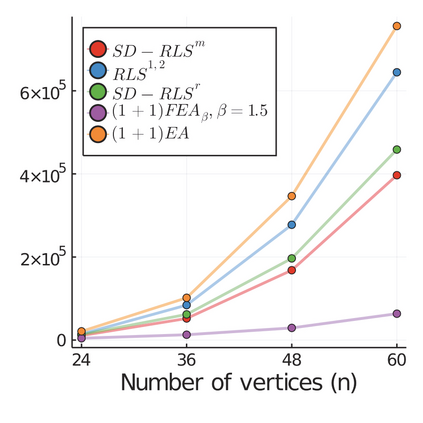
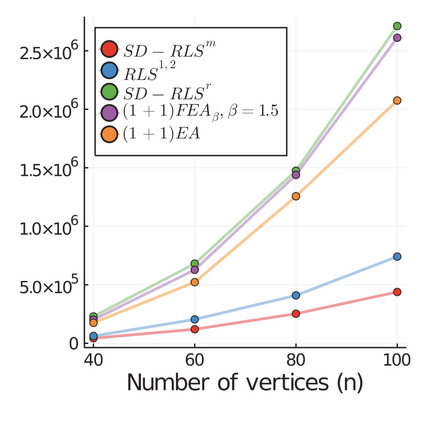
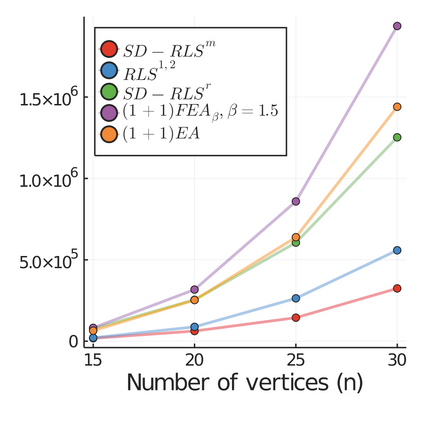
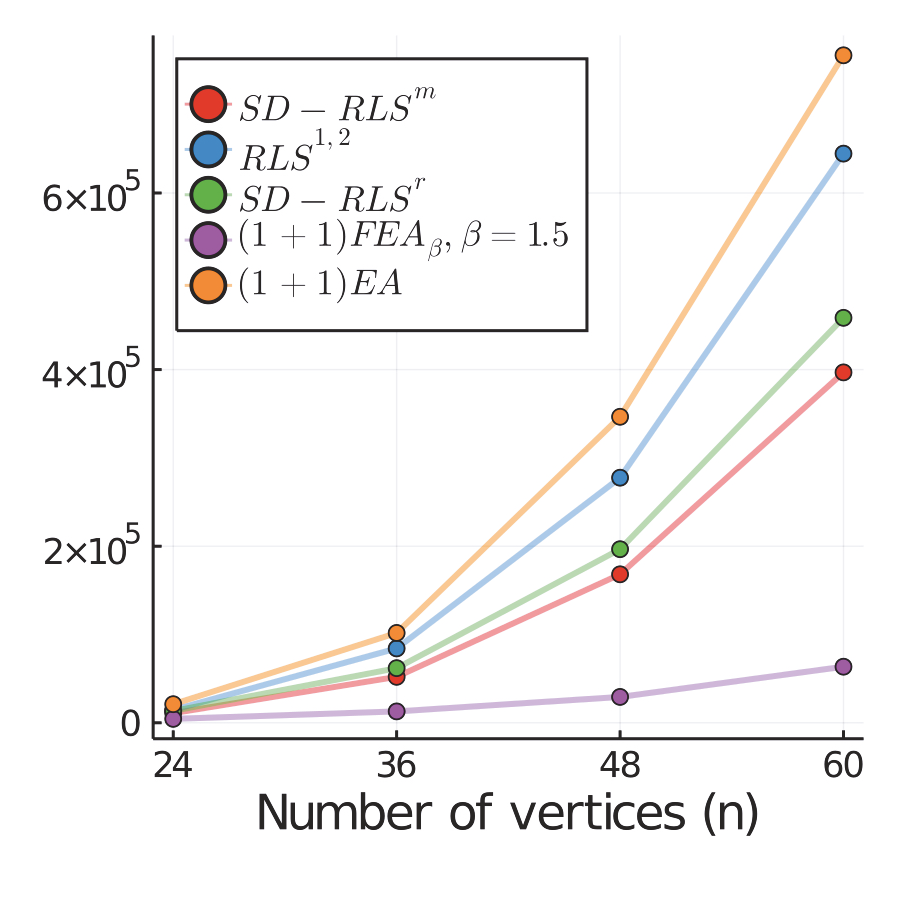
Stagnation detection has been proposed as a mechanism for randomized search heuristics to escape from local optima by automatically increasing the size of the neighborhood to find the so-called gap size, i.e., the distance to the next improvement. Its usefulness has mostly been considered in simple multimodal landscapes with few local optima that could be crossed one after another. In multimodal landscapes with a more complex location of optima of similar gap size, stagnation detection suffers from the fact that the neighborhood size is frequently reset to $1$ without using gap sizes that were promising in the past. In this paper, we investigate a new mechanism called radius memory which can be added to stagnation detection to control the search radius more carefully by giving preference to values that were successful in the past. We implement this idea in an algorithm called SD-RLS$^{\text{m}}$ and show compared to previous variants of stagnation detection that it yields speed-ups for linear functions under uniform constraints and the minimum spanning tree problem. Moreover, its running time does not significantly deteriorate on unimodal functions and a generalization of the Jump benchmark. Finally, we present experimental results carried out to study SD-RLS$^{\text{m}}$ and compare it with other algorithms.
翻译:停滞检测被建议作为一种机制,通过自动增加邻居的面积,以寻找所谓的差距大小,即距离到下一个改进的距离,来随机的搜索超常性以逃离当地选择,从而自动增加邻居的面积,以寻找所谓的差距大小,即距离到下一个改进的距离。其效用主要在简单的多式联运环境中得到考虑,当地选择很少,这种选择可以相互交叉。在比较复杂的偏差大小相近的多式联运环境中,停滞检测受到以下事实的影响:邻居的大小经常被重新设置为1美元,而没有使用过去充满希望的距离大小。在本文中,我们调查一个称为半径内存的新机制,可以添加到停滞检测中,以便更仔细地控制搜索半径,方法是优先考虑过去成功的值。我们用一种称为SD-RLS${text{m ⁇ $} $@m ⁇ $的算法来实施这一想法,并与以往的停滞检测变式相比显示,在统一的制约下和最小的横跨树问题下,它产生线性功能的加速率。此外,它的运行时间在单式功能和跳式基准上并没有严重恶化。最后,我们将实验结果与SDLSD-R_T{lex{@m{@m{x{x}