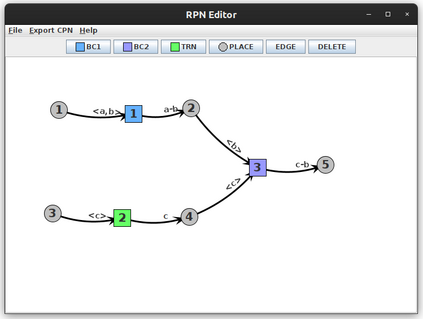
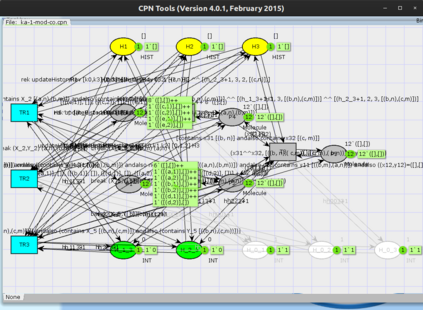
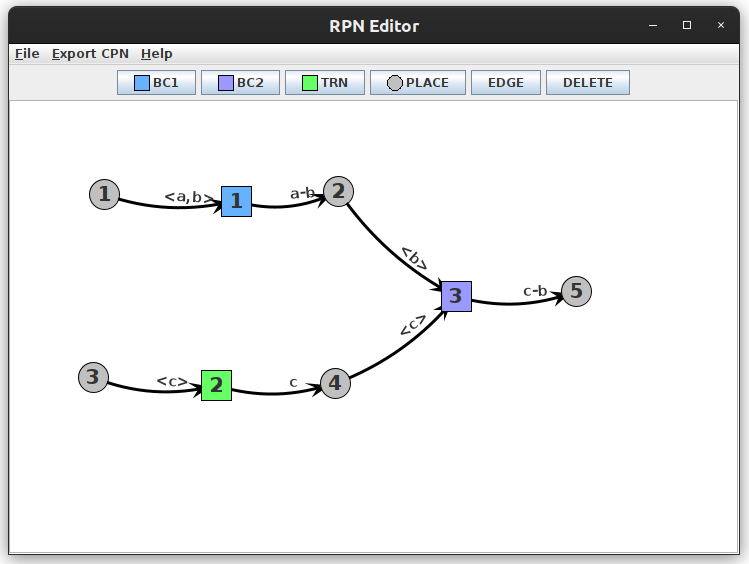
Reversible computation is an emerging computing paradigm that allows any sequence of operations to be executed in reverse order at any point during computation. Its appeal lies in its potential for lowpower computation and its relevance to a wide array of applications such as chemical reactions, quantum computation, robotics, and distributed systems. Reversing Petri nets are a recently-proposed extension of Petri nets that implements the three main forms of reversibility, namely, backtracking, causal reversing, and out-of-causal-order reversing. Their distinguishing feature is the use of named tokens that can be combined together to form bonds. Named tokens along with a history function, constitute the means of remembering past behaviour, thus, enabling reversal. In recent work, we have proposed a structural translation from a subclass of RPNs to the model of Coloured Petri Nets (CPNs), an extension of traditional Petri nets where tokens carry data values. In this paper, we extend the translation to handle RPNs with token multiplicity under the individual-token interpretation, a model which allows multiple tokens of the same type to exist in a system. To support the three types of reversibility, tokens are associated with their causal history and, while tokens of the same type are equally eligible to fire a transition when going forward, when going backwards they are able to reverse only the transitions they have previously fired. The new translation, in addition to lifting the restriction on token uniqueness, presents a refined approach for transforming RPNs to CPNs through a unifying approach that allows instantiating each of the three types of reversibility. The paper also reports on a tool that implements this translation, paving the way for automated translations and analysis of reversible systems using CPN Tools.
翻译:暂无翻译