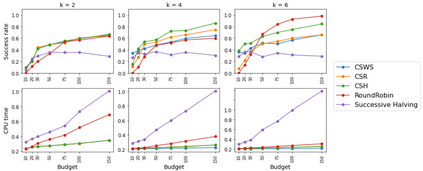
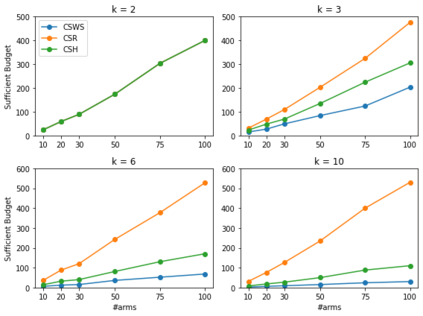
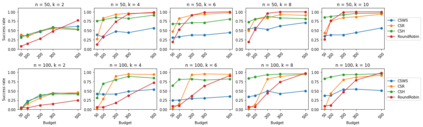
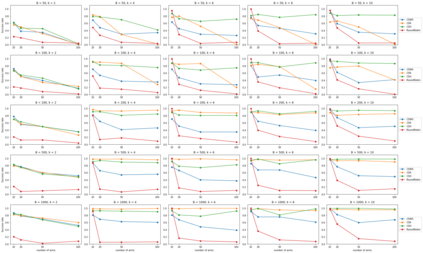
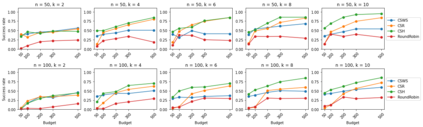
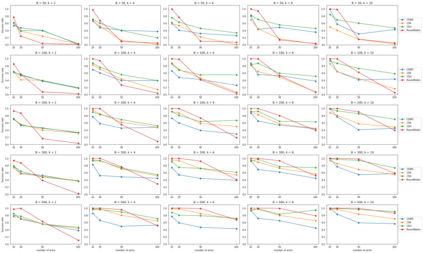
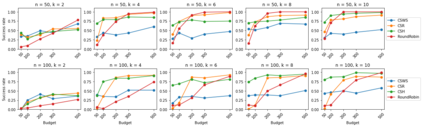
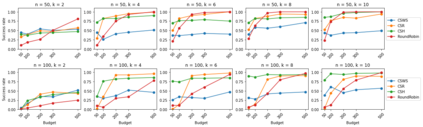
We consider the combinatorial bandits problem with semi-bandit feedback under finite sampling budget constraints, in which the learner can carry out its action only for a limited number of times specified by an overall budget. The action is to choose a set of arms, whereupon feedback for each arm in the chosen set is received. Unlike existing works, we study this problem in a non-stochastic setting with subset-dependent feedback, i.e., the semi-bandit feedback received could be generated by an oblivious adversary and also might depend on the chosen set of arms. In addition, we consider a general feedback scenario covering both the numerical-based as well as preference-based case and introduce a sound theoretical framework for this setting guaranteeing sensible notions of optimal arms, which a learner seeks to find. We suggest a generic algorithm suitable to cover the full spectrum of conceivable arm elimination strategies from aggressive to conservative. Theoretical questions about the sufficient and necessary budget of the algorithm to find the best arm are answered and complemented by deriving lower bounds for any learning algorithm for this problem scenario.
翻译:我们认为,在有限的抽样预算限制下,学习者只能在总预算规定的有限时间内采取行动。行动是选择一套武器,从中接收对所选每股手臂的反馈。与现有的工作不同,我们在非随机环境中研究这一问题,有亚集依赖的反馈,即收到的半海底反馈可能由不为人知的对手产生,也可能取决于所选择的一套武器。此外,我们考虑一种一般的反馈设想,既包括以数字为基础的案例,也包括以优惠为基础的案例,并为这一设定引入一个健全的理论框架,保证最佳武器的合理概念,一个学习者试图找到这种概念。我们建议一种通用算法,适合于涵盖从侵略到保守的可想象的消除武器战略的全部范围。关于算法找到最佳手臂的充足和必要的预算的理论问题,通过为这一问题情景的任何学习算法确定较低的界限而得到解答和补充。