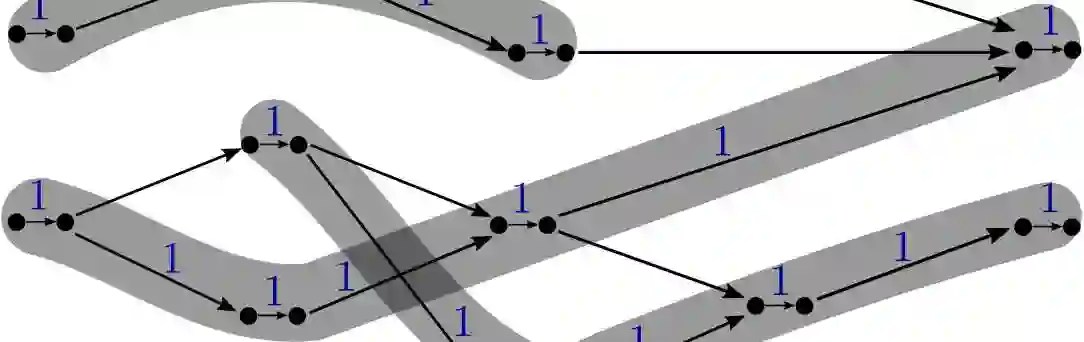
A minimum path cover (MPC) of a directed acyclic graph (DAG) $G = (V,E)$ is a minimum-size set of paths that together cover all the vertices of the DAG. Computing an MPC is a basic polynomial problem, dating back to Dilworth's and Fulkerson's results in the 1950s. Since the size $k$ of an MPC (also known as the width) can be small in practical applications, research has also studied algorithms whose running time is parameterized on $k$. We obtain a new MPC parameterized algorithm for DAGs running in time $O(k^2|V| + |E|)$. Our algorithm is the first solving the problem in parameterized linear time. Additionally, we obtain an edge sparsification algorithm preserving the width of a DAG but reducing $|E|$ to less than $2|V|$. This algorithm runs in time $O(k^2|V|)$ and requires an MPC of a DAG as input, thus its total running time is the same as the running time of our MPC algorithm.
翻译:定向自行车图(DAG) $G = (V,E) = (V,E) 的最小路径覆盖(MPC) 是一套最小尺寸的路径, 共覆盖DAG的所有顶点。 计算一个 MPC 是一个基本的多元问题, 追溯到 Dilworth 和 Fulketerson 1950年代的结果。 由于MPC (又称宽度) 的大小在实际应用中可能很小, 研究还研究了运行时间以美元为参数的算法。 我们为在时间运行的 DAG 获得一个新的 MPC 参数化算法 $O (k ⁇ 2 ⁇ V ⁇ + ⁇ E ⁇ ) $。 我们的算法是第一个解决参数线性时间问题的方法。 此外, 我们得到了一种边缘宽度算法, 保存 DAG 的宽度, 但它将 $E ⁇ $ 减到 $@v ⁇ $ 。 这种算法将时间用 $O (k) =2 ⁇ V} 并需要 MPC MPC 作为输入, 因此其总运行时间与 MPC MAC 算法相同。