Adaptation using spatially distributed Gaussian Processes

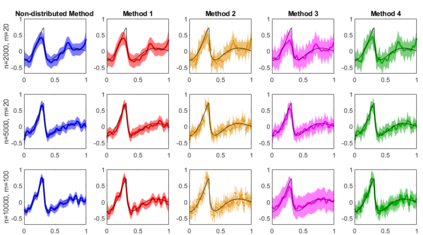
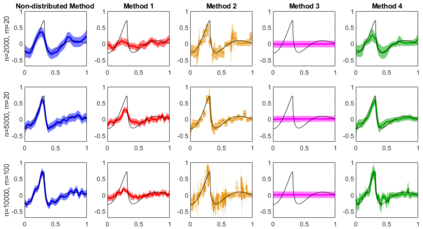
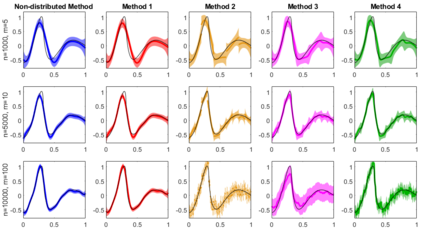
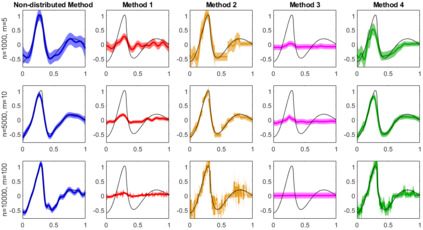
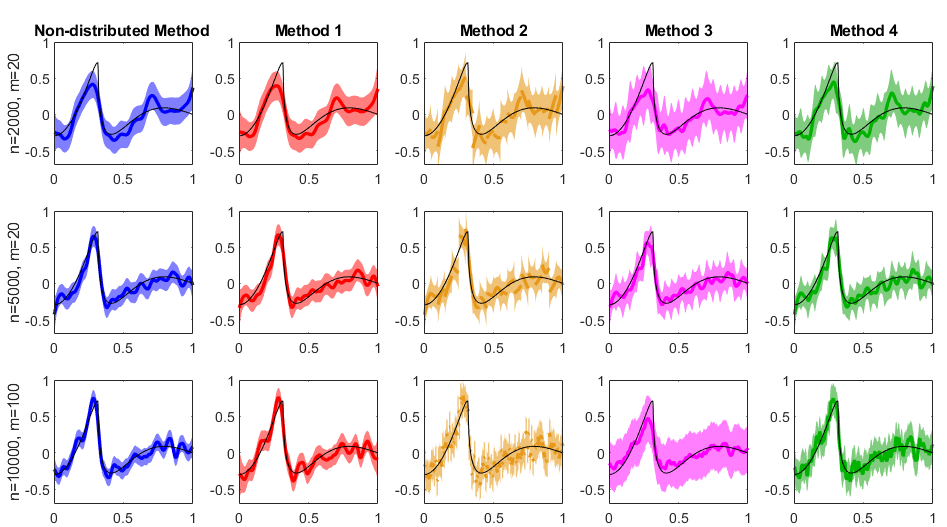
We consider the accuracy of an approximate posterior distribution in nonparametric regression problems by combining posterior distributions computed on subsets of the data defined by the locations of the independent variables. We show that this approximate posterior retains the rate of recovery of the full data posterior distribution, where the rate of recovery adapts to the smoothness of the true regression function. As particular examples we consider Gaussian process priors based on integrated Brownian motion and the Mat\'ern kernel augmented with a prior on the length scale. Besides theoretical guarantees we present a numerical study of the methods both on synthetic and real world data. We also propose a new aggregation technique, which numerically outperforms previous approaches.