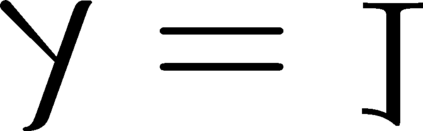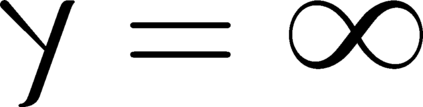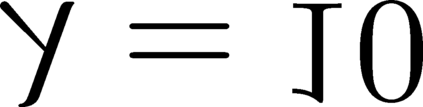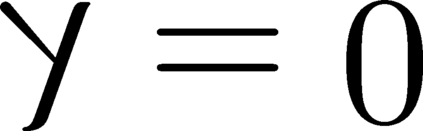Modern inference and learning often hinge on identifying low-dimensional structures that approximate large scale data. Subspace clustering achieves this through a union of linear subspaces. However, in contemporary applications data is increasingly often incomplete, rendering standard (full-data) methods inapplicable. On the other hand, existing incomplete-data methods present major drawbacks, like lifting an already high-dimensional problem, or requiring a super polynomial number of samples. Motivated by this, we introduce a new subspace clustering algorithm inspired by fusion penalties. The main idea is to permanently assign each datum to a subspace of its own, and minimize the distance between the subspaces of all data, so that subspaces of the same cluster get fused together. Our approach is entirely new to both, full and missing data, and unlike other methods, it directly allows noise, it requires no liftings, it allows low, high, and even full-rank data, it approaches optimal (information-theoretic) sampling rates, and it does not rely on other methods such as low-rank matrix completion to handle missing data. Furthermore, our extensive experiments on both real and synthetic data show that our approach performs comparably to the state-of-the-art with complete data, and dramatically better if data is missing.
翻译:现代推论和学习往往取决于如何识别接近大比例数据的低维结构。 子空间集群通过线性子空间的组合来实现这一点。 但是, 在当代应用数据中,数据往往越来越不完善,使得标准(完整数据)方法无法适用。 另一方面, 现有的不完全数据方法存在重大缺陷, 比如提升一个已经高层次的问题, 或者需要超多级的样本数量。 受此驱动, 我们引入了一种受聚变罚款启发的新的子空间组合算法。 其主要想法是永久地将每个数据都分配到自己的子空间, 并尽可能缩小所有数据子空间之间的距离, 从而使同一组的子空间相互连接起来。 此外, 我们的方法对于全部和缺失的数据都是全新的, 与其他方法不同, 它直接允许噪音, 它不需要提升, 它允许低、 高甚至全位的数据, 它接近最佳( 信息理论性) 取样率, 它并不依赖诸如低级别矩阵完成处理缺失数据的其他方法。 此外, 我们对于真实和合成数据进行的广泛实验, 如果真实的和合成数据都显示我们完全的状态, 我们对于真实和完整的数据进行更精确的实验, 则显示我们完全的数据进行。