Sequential Learning of the Topological Ordering for the Linear Non-Gaussian Acyclic Model with Parametric Noise

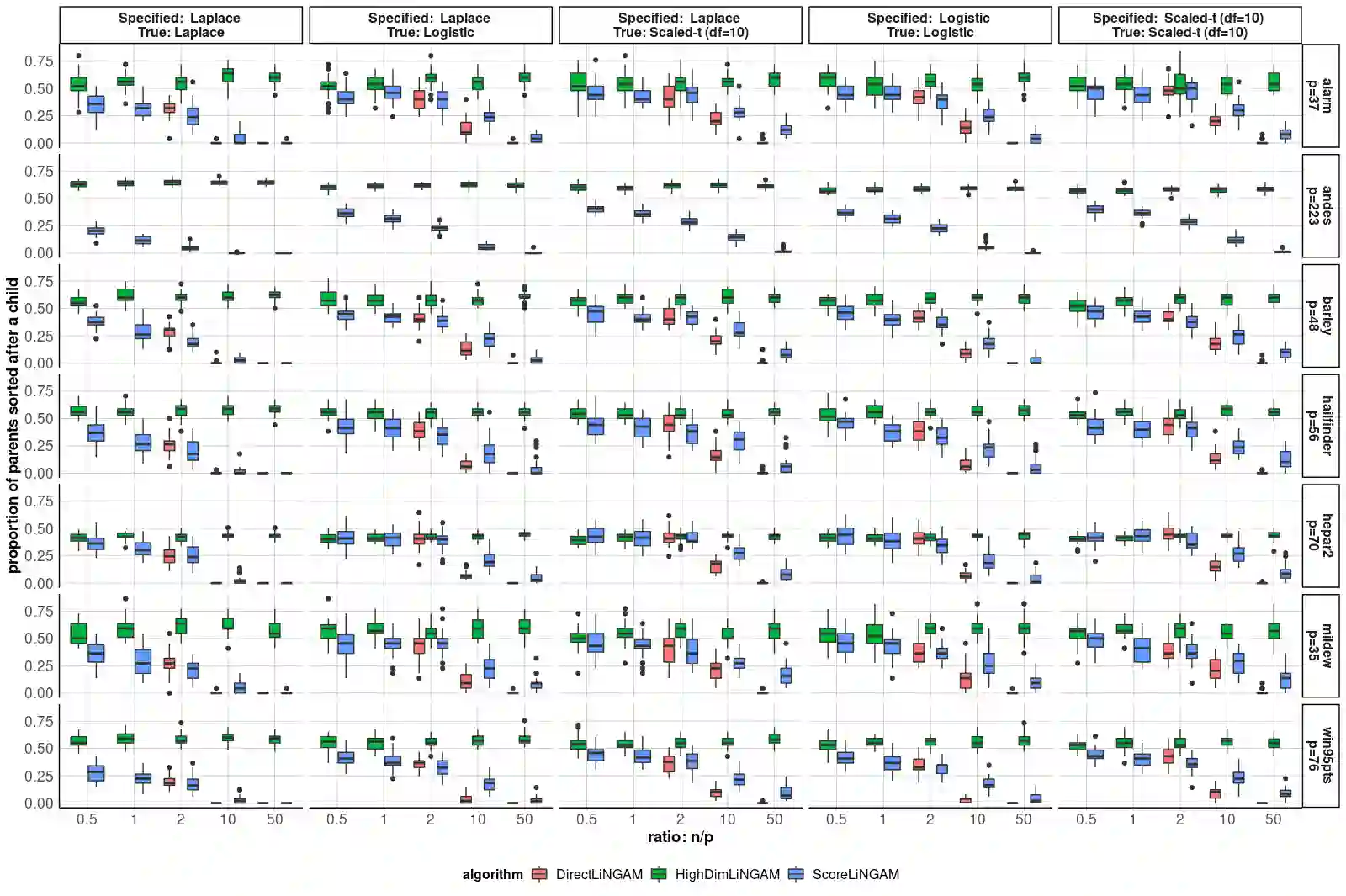
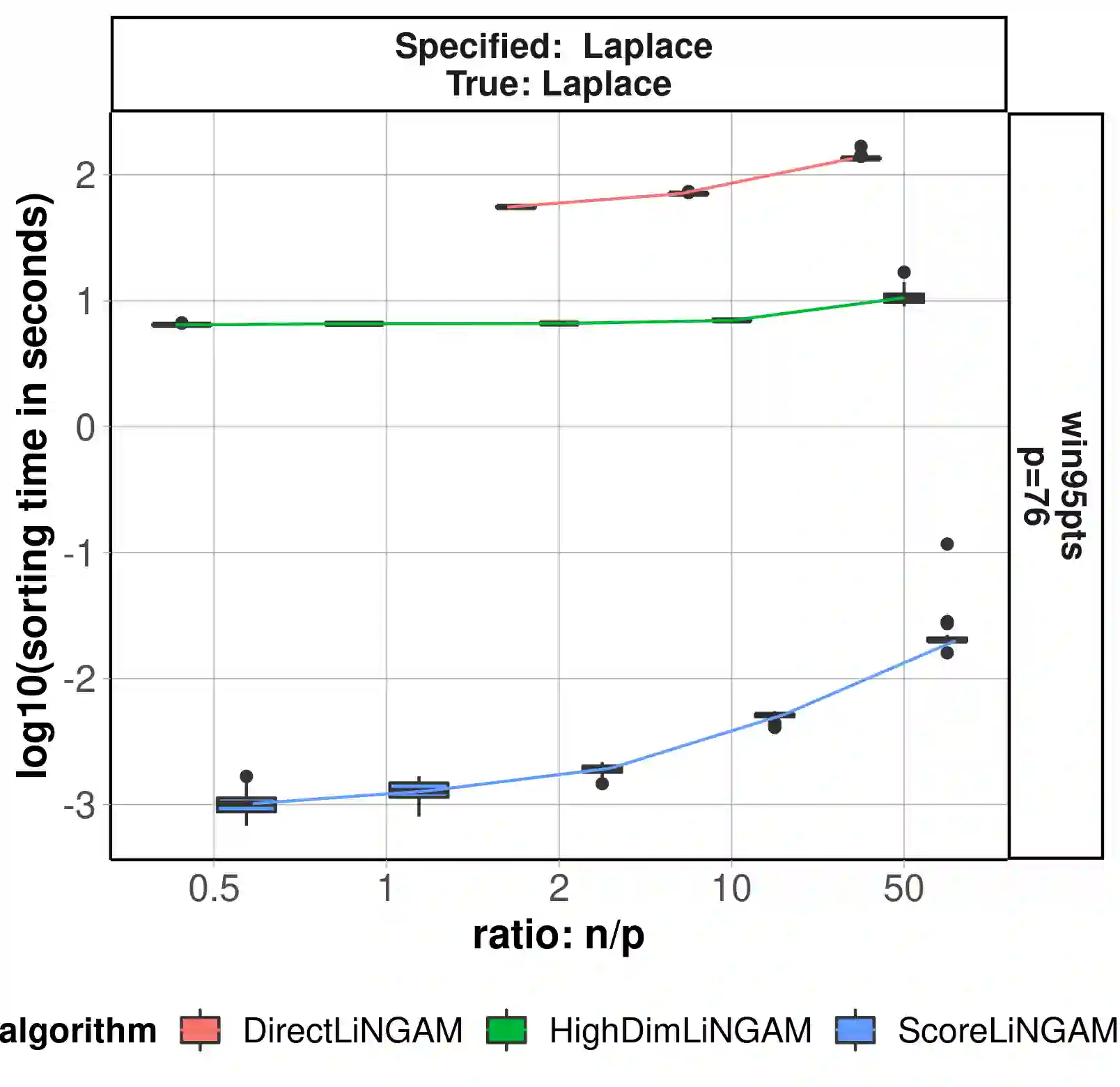
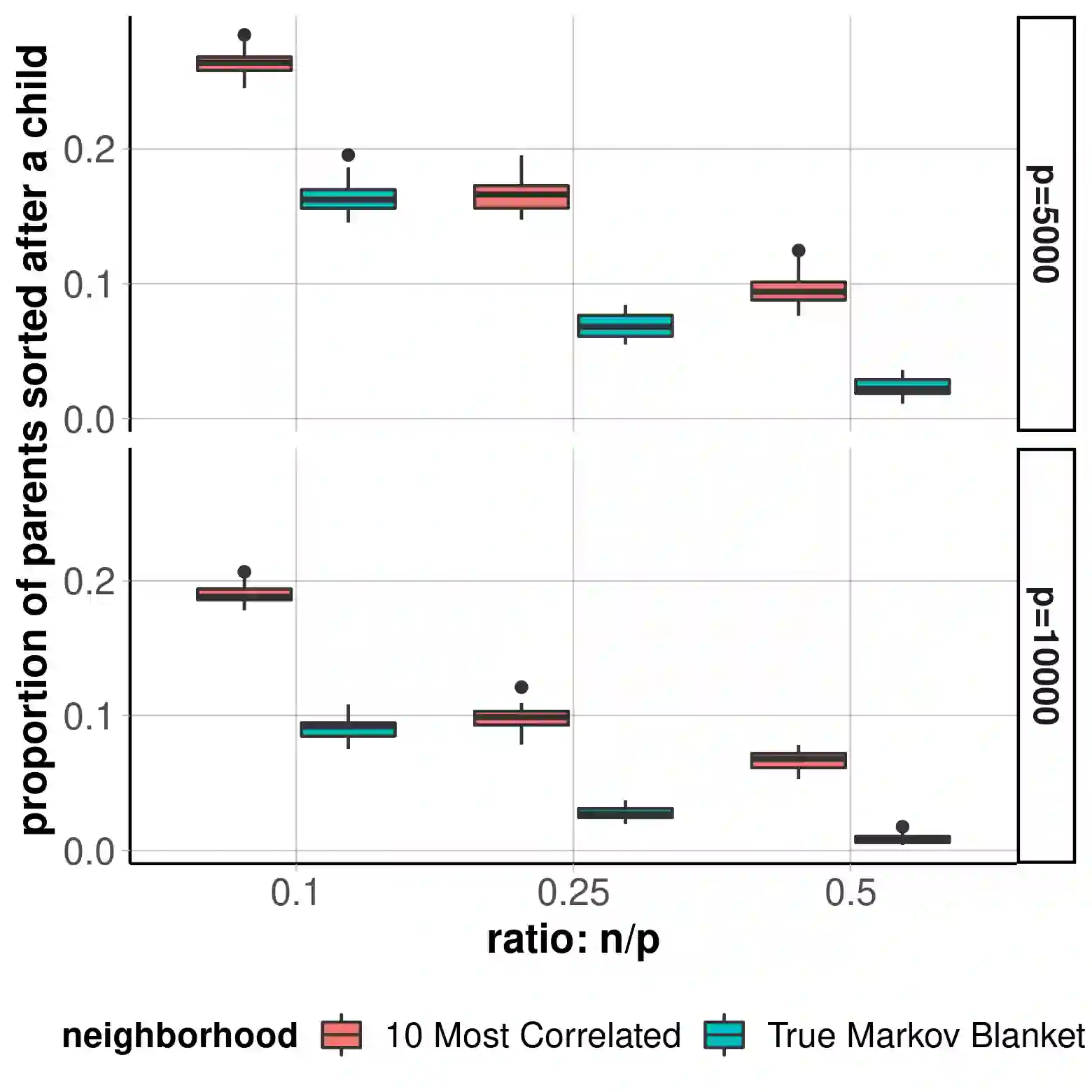
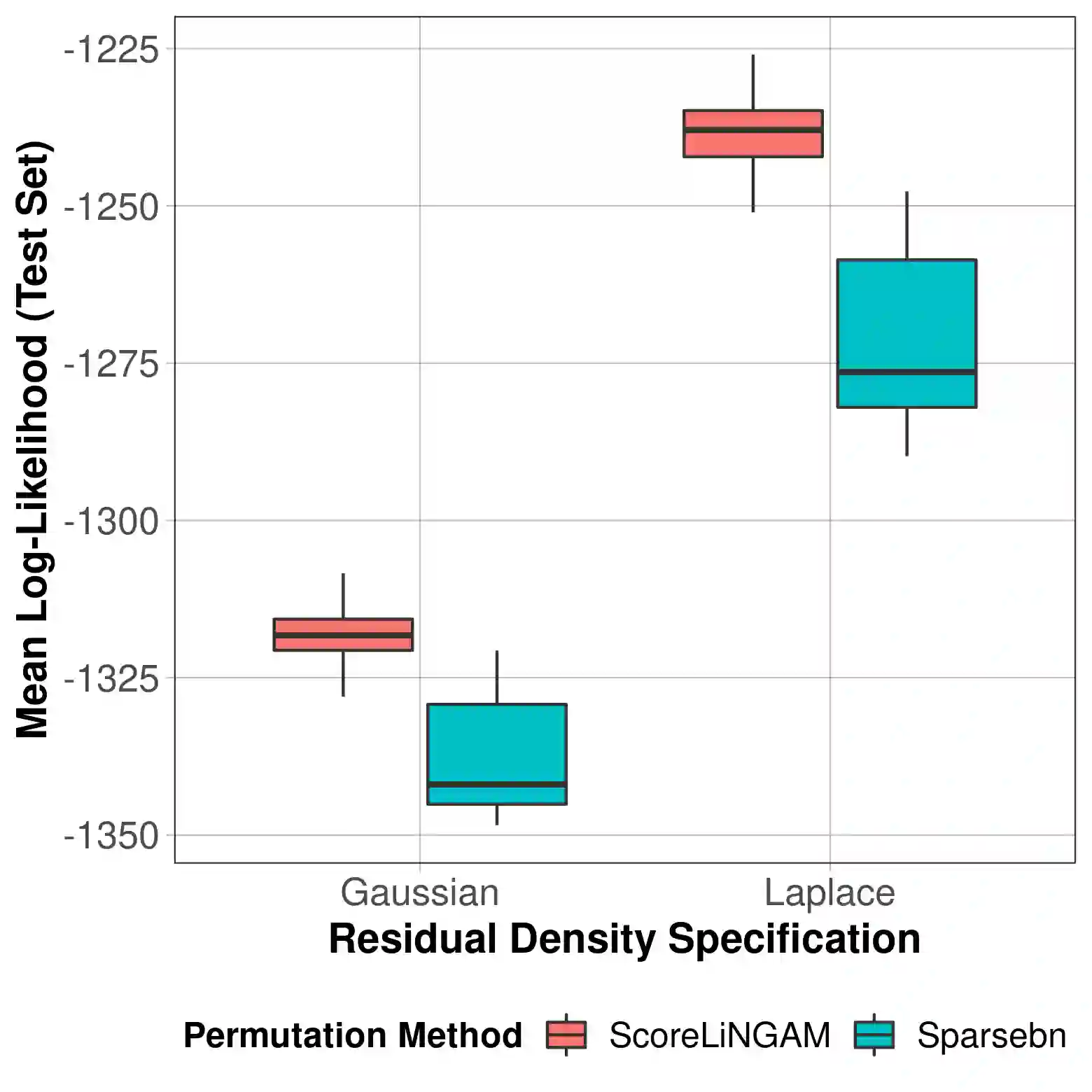
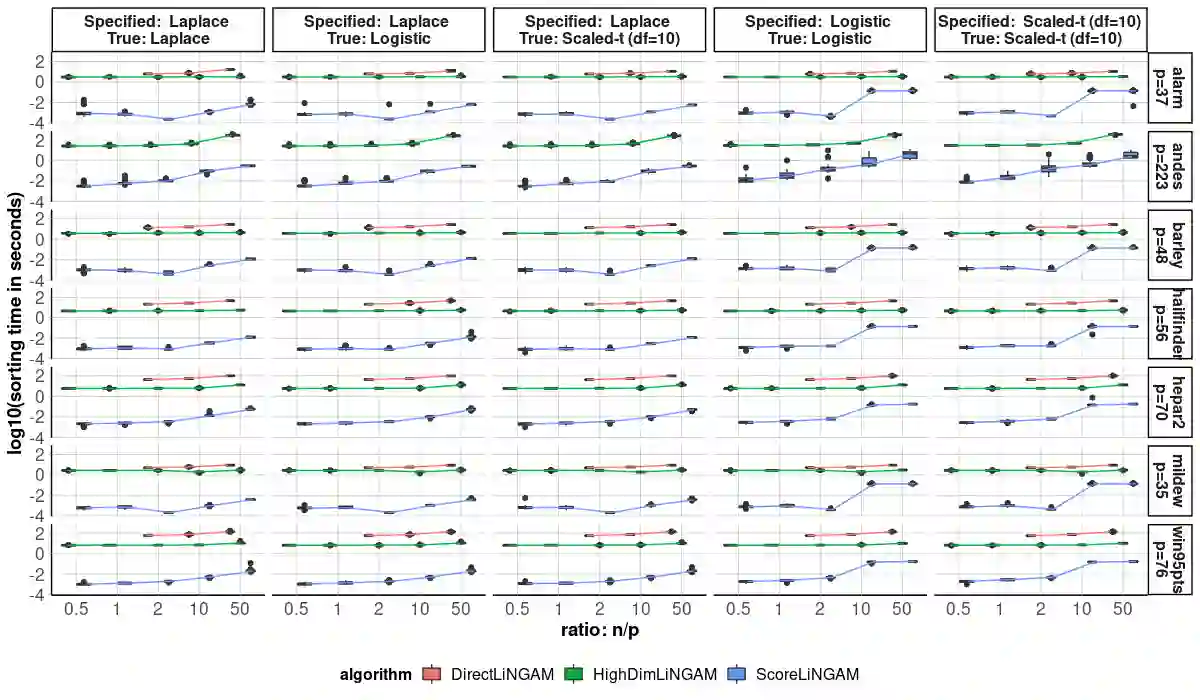
Causal discovery, the learning of causality in a data mining scenario, has been of strong scientific and theoretical interest as a starting point to identify "what causes what?" Contingent on assumptions, it is sometimes possible to identify an exact causal Directed Acyclic Graph (DAG), as opposed to a Markov equivalence class of graphs that gives ambiguity of causal directions. The focus of this paper is on one such case: a linear structural equation model with non-Gaussian noise, a model known as the Linear Non-Gaussian Acyclic Model (LiNGAM). Given a specified parametric noise model, we develop a novel sequential approach to estimate the causal ordering of a DAG. At each step of the procedure, only simple likelihood ratio scores are calculated on regression residuals to decide the next node to append to the current partial ordering. Under mild assumptions, the population version of our procedure provably identifies a true ordering of the underlying causal DAG. We provide extensive numerical evidence to demonstrate that our sequential procedure is scalable to cases with possibly thousands of nodes and works well for high-dimensional data. We also conduct an application to a single-cell gene expression dataset to demonstrate our estimation procedure.