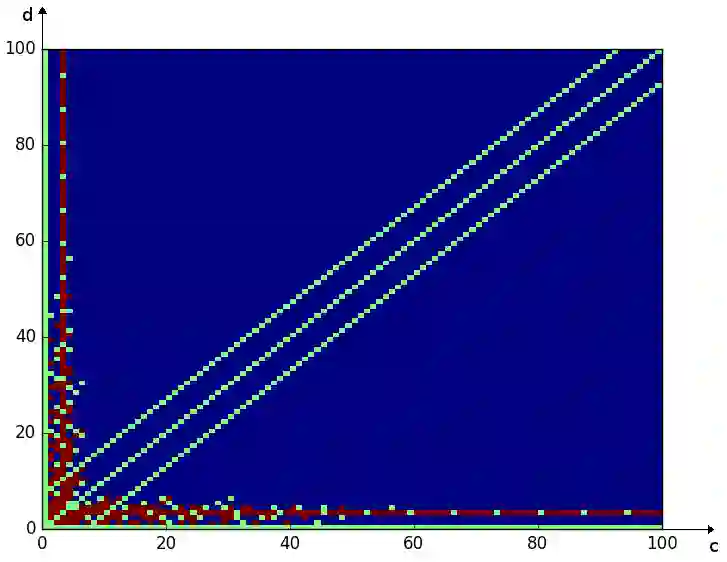
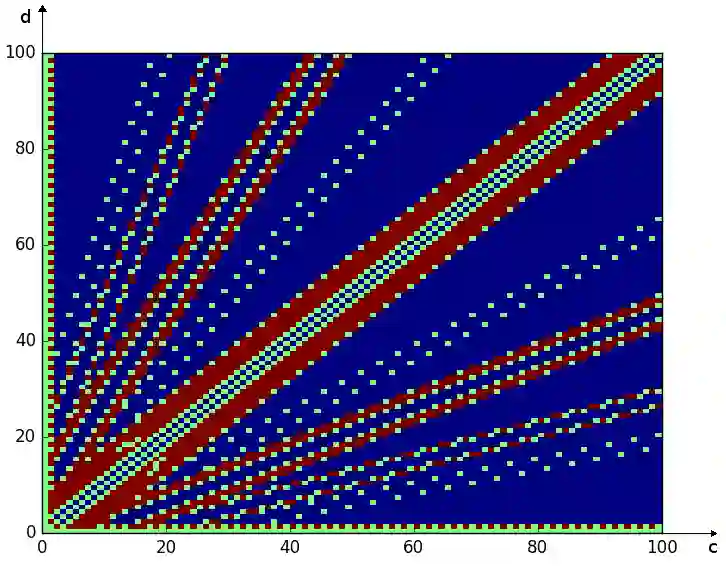
Partizan 减法游戏 (Partizan Subtraction Games)

Partizan subtraction games are combinatorial games where two players, say Left and Right, alternately remove a number n of tokens from a heap of tokens, with $n \in S_L$ (resp. $n \in S_R$) when it is Left's (resp. Right's) turn. The first player unable to move loses. These games were introduced by Fraenkel and Kotzig in 1987, where they introduced the notion of dominance, i.e. an asymptotic behavior of the outcome sequence where Left always wins if the heap is sufficiently large. In the current paper, we investigate the other kinds of behaviors for the outcome sequence. In addition to dominance, three other disjoint behaviors are defined, namely weak dominance, fairness and ultimate impartiality. We consider the problem of computing this behavior with respect to $S_L$ and $S_R$, which is connected to the well-known Frobenius coin problem. General results are given, together with arithmetic and geometric characterizations when the sets $S_L$ and $S_R$ have size at most 2.

翻译：partizan 减法游戏是组合式游戏, 其中两个玩家, 比如左键和右键, 交替地从牌状堆中去除若干n 符号。当左键翻转( resp. $n s_ in S_ R$) 时, 当左键翻转( resp. 右键) 时, partizan 减法游戏是组合式游戏。第一个无法移动的玩家是损失。这些游戏是由 Fraenkel 和 Kotzig 于1987 年引入的, 其中他们引入了主导性的概念, 即如果堆积足够大, 左键总是赢的结果序列的不严谨行为。在当前的文件中, 我们调查结果序列中的结果序列的其他行为类型。除了主导性外, 其它三种不合作的行为定义, 即弱支配性、公正和最终公正性。我们考虑计算此行为的问题, $S_ 和 $S_ 和 $S_ R$ 问题, 它与众所周知的 Frobenius 硬币问题有关。。。。一般的结果与算算和几组和几数描述的大小最多为2 。