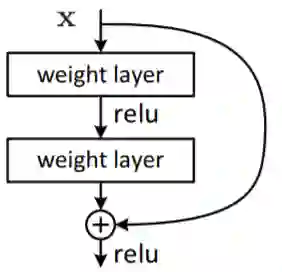
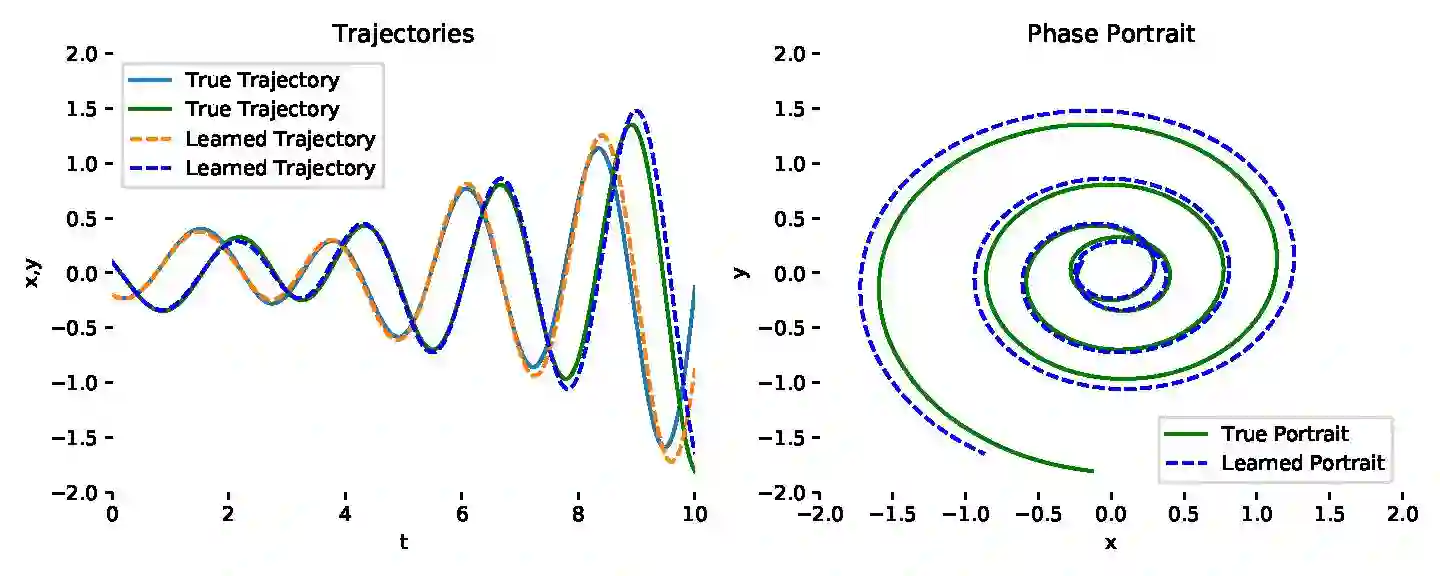
Neural ordinary differential equations (NODEs) treat computation of intermediate feature vectors as trajectories of ordinary differential equation parameterized by a neural network. In this paper, we propose a novel model, delay differential neural networks (DDNN), inspired by delay differential equations (DDEs). The proposed model considers the derivative of the hidden feature vector as a function of the current feature vector and past feature vectors (history). The function is modelled as a neural network and consequently, it leads to continuous depth alternatives to many recent ResNet variants. We propose two different DDNN architectures, depending on the way current and past feature vectors are considered. For training DDNNs, we provide a memory-efficient adjoint method for computing gradients and back-propagate through the network. DDNN improves the data efficiency of NODE by further reducing the number of parameters without affecting the generalization performance. Experiments conducted on synthetic and real-world image classification datasets such as Cifar10 and Cifar100 show the effectiveness of the proposed models.
翻译:神经普通差分方程式(NODEs)将中间特性矢量的计算作为神经网络中普通差别方程式参数的轨迹。在本文中,我们提出了一个新型模型,即延迟差异神经网络(DDNN),由延迟差分方程(DDEs)启发。拟议模型认为隐藏特性矢量的衍生物是当前特性矢量和过去特性矢量(历史)的函数。该功能以神经网络为模型,因此,它导致与最近许多ResNet变量相较的连续深度替代物。我们建议了两种不同的DNNN结构,这取决于考虑当前和过去特性矢量的方式。关于DNNTs的培训,我们为通过网络计算梯度和后方程式提供了一种记忆高效的共用方法。DNNNNE通过进一步减少参数数量而不影响通用性能,从而提高了NOD的数据效率。在Cifar10和Cifar100等合成和真实世界图像分类数据集上进行的实验显示了拟议模型的有效性。