The Price of Anarchy is Fragile in Single-Selection Coverage Games

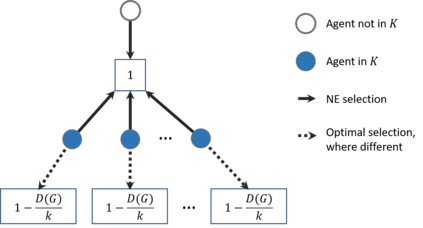
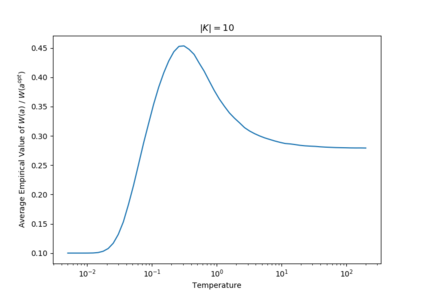
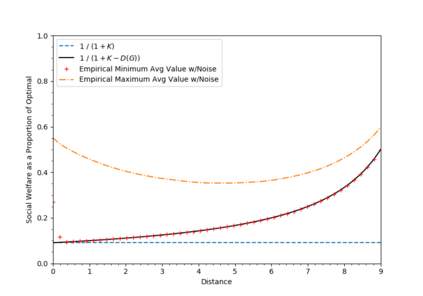
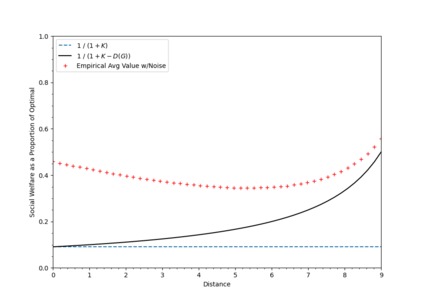
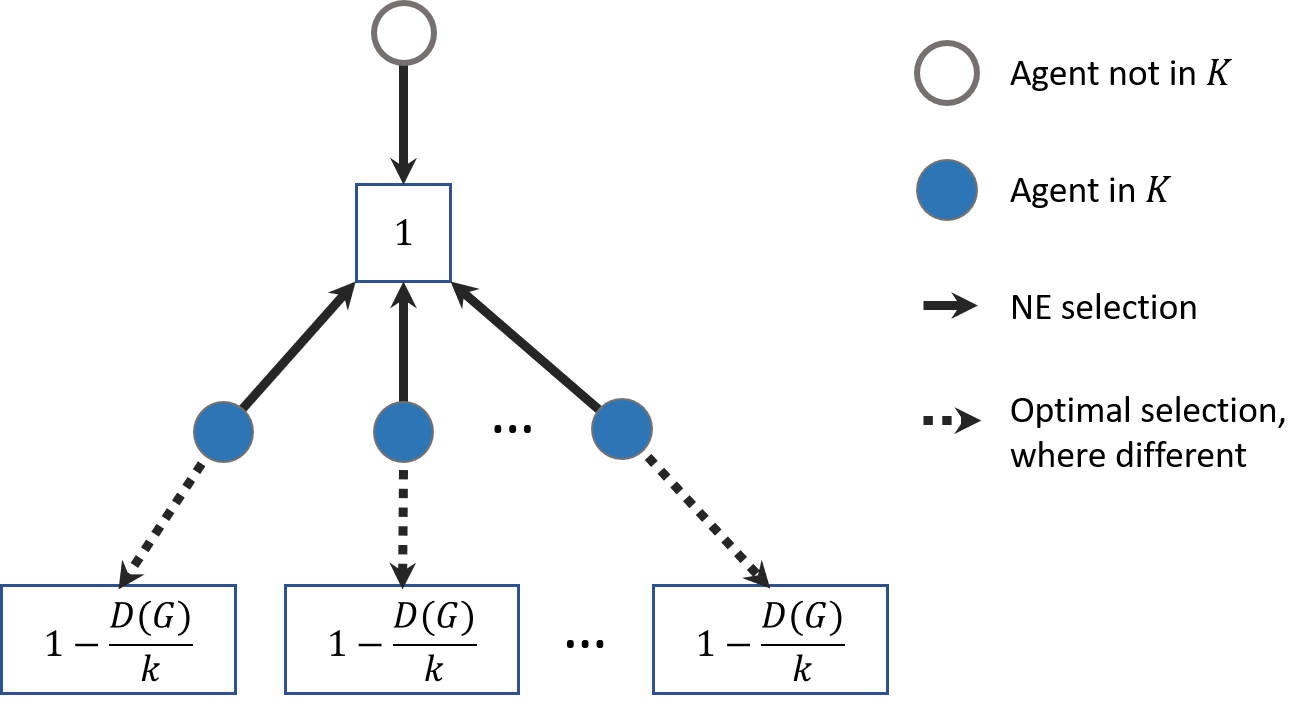
This paper considers coverage games in which a group of agents are tasked with identifying the highest-value subset of resources; in this context, game-theoretic approaches are known to yield Nash equilibria within a factor of 2 of optimal. We consider the case that some of the agents suffer a communication failure and cannot observe the actions of other agents; in this case, recent work has shown that if there are k>0 compromised agents, Nash equilibria are only guaranteed to be within a factor of k+1 of optimal. However, the present paper shows that this worst-case guarantee is fragile; in a sense which we make precise, we show that if a problem instance has a very poor worst-case guarantee, then it is necessarily very "close" to a problem instance with an optimal Nash equilibrium. Conversely, an instance that is far from one with an optimal Nash equilibrium necessarily has relatively good worst-case performance guarantees. To contextualize this fragility, we perform simulations using the log-linear learning algorithm and show that average performance on worst-case instances is considerably better even than our improved analytical guarantees. This suggests that the fragility of the price of anarchy can be exploited algorithmically to compensate for online communication failures.