Analysing Multiscale Clusterings with Persistent Homology

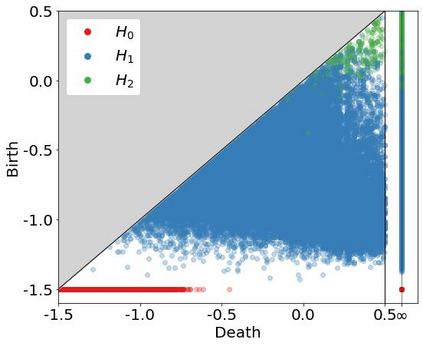
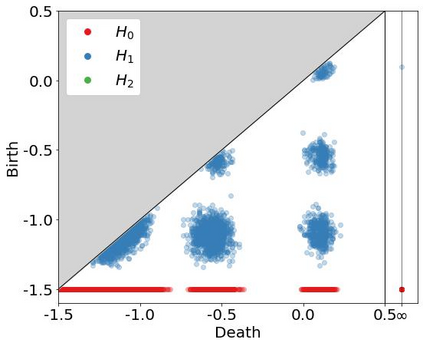
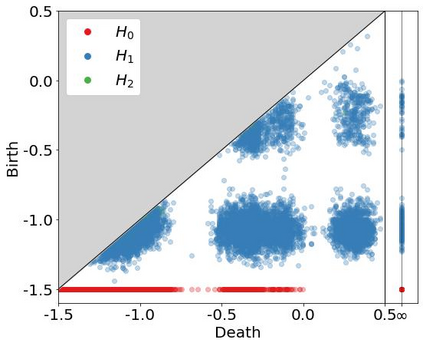
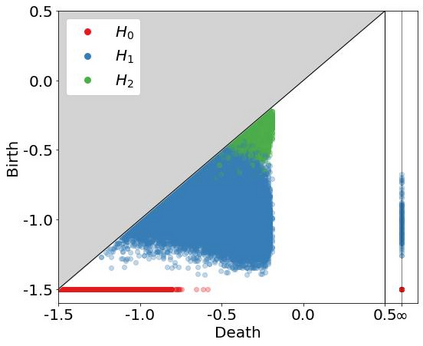
In many applications in data clustering, it is desirable to find not just a single partition into clusters but a sequence of partitions describing the data at different scales (or levels of coarseness). A natural problem then is to analyse and compare the (not necessarily hierarchical) sequences of partitions that underpin multiscale descriptions of data. Here, we introduce the Multiscale Clustering Filtration (MCF), a well-defined and stable filtration of abstract simplicial complexes that encodes arbitrary patterns of cluster assignments across scales of increasing coarseness. We show that the zero-dimensional persistent homology of the MCF measures the degree of hierarchy in the sequence of partitions, and the higher-dimensional persistent homology tracks the emergence and resolution of conflicts between cluster assignments across the sequence of partitions. To broaden the theoretical foundations of the MCF, we also provide an equivalent construction via a nerve complex filtration, and we show that in the hierarchical case, the MCF reduces to a Vietoris-Rips filtration of an ultrametric space. We then use numerical experiments to illustrate how the MCF can serve to characterise multiscale clusterings of synthetic data from stochastic block models.