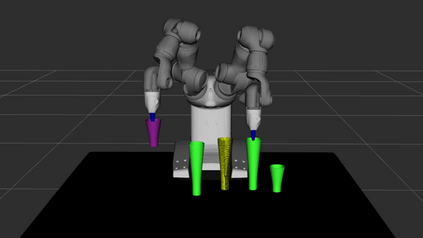
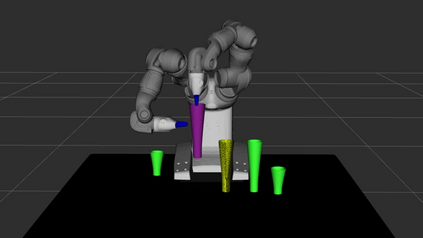
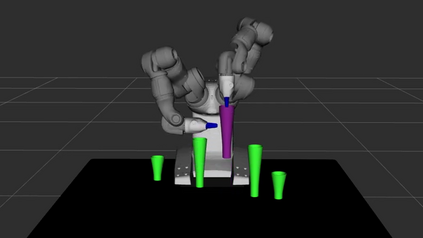
Replanners are efficient methods for solving non-deterministic planning problems. Despite showing good scalability, existing replanners often fail to solve problems involving a large number of misleading plans, i.e., weak plans that do not lead to strong solutions, however, due to their minimal lengths, are likely to be found at every replanning iteration. The poor performance of replanners in such problems is due to their all-outcome determinization. That is, when compiling from non-deterministic to classical, they include all compiled classical operators in a single deterministic domain which leads replanners to continually generate misleading plans. We introduce an offline replanner, called Safe-Planner (SP), that relies on a single-outcome determinization to compile a non-deterministic domain to a set of classical domains, and ordering heuristics for ranking the obtained classical domains. The proposed single-outcome determinization and the heuristics allow for alternating between different classical domains. We show experimentally that this approach can allow SP to avoid generating misleading plans but to generate weak plans that directly lead to strong solutions. The experiments show that SP outperforms state-of-the-art non-deterministic solvers by solving a broader range of problems. We also validate the practical utility of SP in real-world non-deterministic robotic tasks.
翻译:重新规划者是解决非确定性规划问题的高效方法。尽管现有重新规划者表现出了良好的可伸缩性,但往往无法解决涉及大量误导性计划的问题,即,由于时间长度最小,在每次重新规划迭代时都可能发现计划不力,然而,由于时间长度最小,很可能发现每个重新规划者都无法找到强有力的解决办法。重规划者在这类问题上表现不佳的原因是他们获得了全部结果的确定性。这就是说,在从非确定性汇编到经典时,它们包括所有编集的古典操作者,它们都包含在一个单一的确定性域中,导致再规划者不断产生误导性计划。我们引入了离线性重规划者,称为安全计划(SP),依靠单一结果确定性确定性,将非确定性领域编集成一套传统领域,并下令对获得的经典域进行排位。拟议的单一结果确定性确定性和超自然论允许在不同的经典域中进行交替。我们实验显示,这种方法可以让SP避免产生误导性计划,但能够产生更宽泛的虚拟性任务,从而直接地解决非决定性版域域域域域域性研究问题。