A Spectral Approach to Polytope Diameter

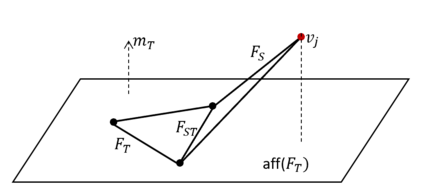
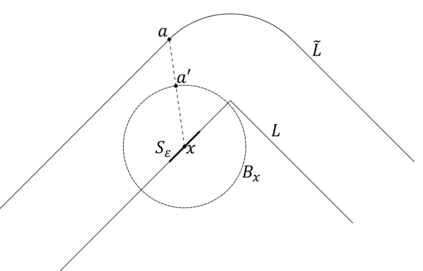
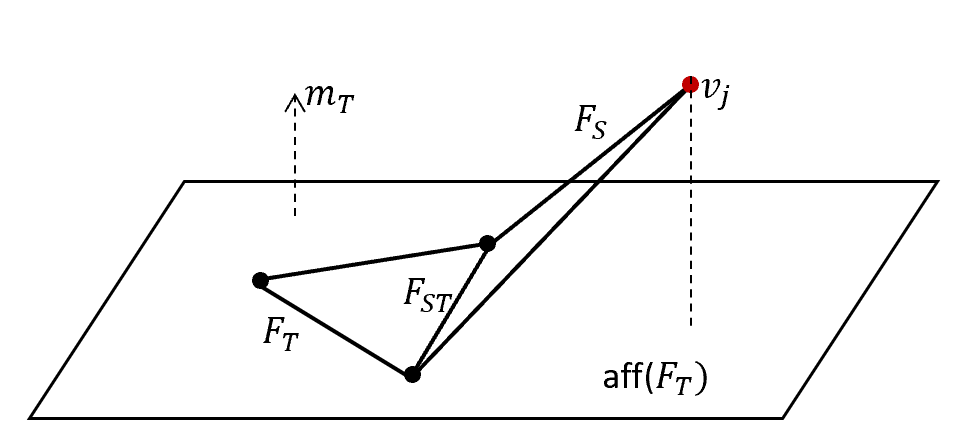
We prove upper bounds on the graph diameters of polytopes in two settings. The first is a worst-case bound for integer polytopes in terms of the length of the description of the polytope (in bits) and the minimum angle between facets of its polar. The second is a smoothed analysis bound: given an appropriately normalized polytope, we add small Gaussian noise to each constraint. We consider a natural geometric measure on the vertices of the perturbed polytope (corresponding to the mean curvature measure of its polar) and show that with high probability there exists a "giant component" of vertices, with measure $1-o(1)$ and polynomial diameter. Both bounds rely on spectral techniques -- applied to a certain matrix in the first case, and a certain continuous time Markov chain in the second. The necessary spectral gap bounds arise from the log-concavity of the volume of a simple polytope in terms of its slack variables, which is extended to non-simple polytopes via an approximation argument.