Fast approximation of orthogonal matrices and application to PCA

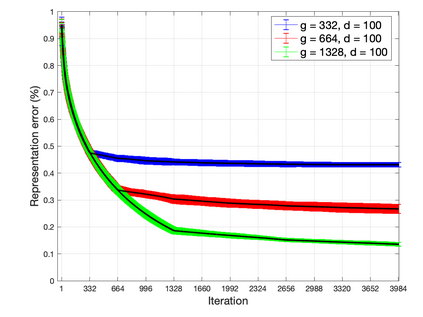
We study the problem of approximating orthogonal matrices so that their application is numerically fast and yet accurate. We find an approximation by solving an optimization problem over a set of structured matrices, that we call extended orthogonal Givens transformations, including Givens rotations as a special case. We propose an efficient greedy algorithm to solve such a problem and show that it strikes a balance between approximation accuracy and speed of computation. The approach is relevant to spectral methods and we illustrate its application to PCA.