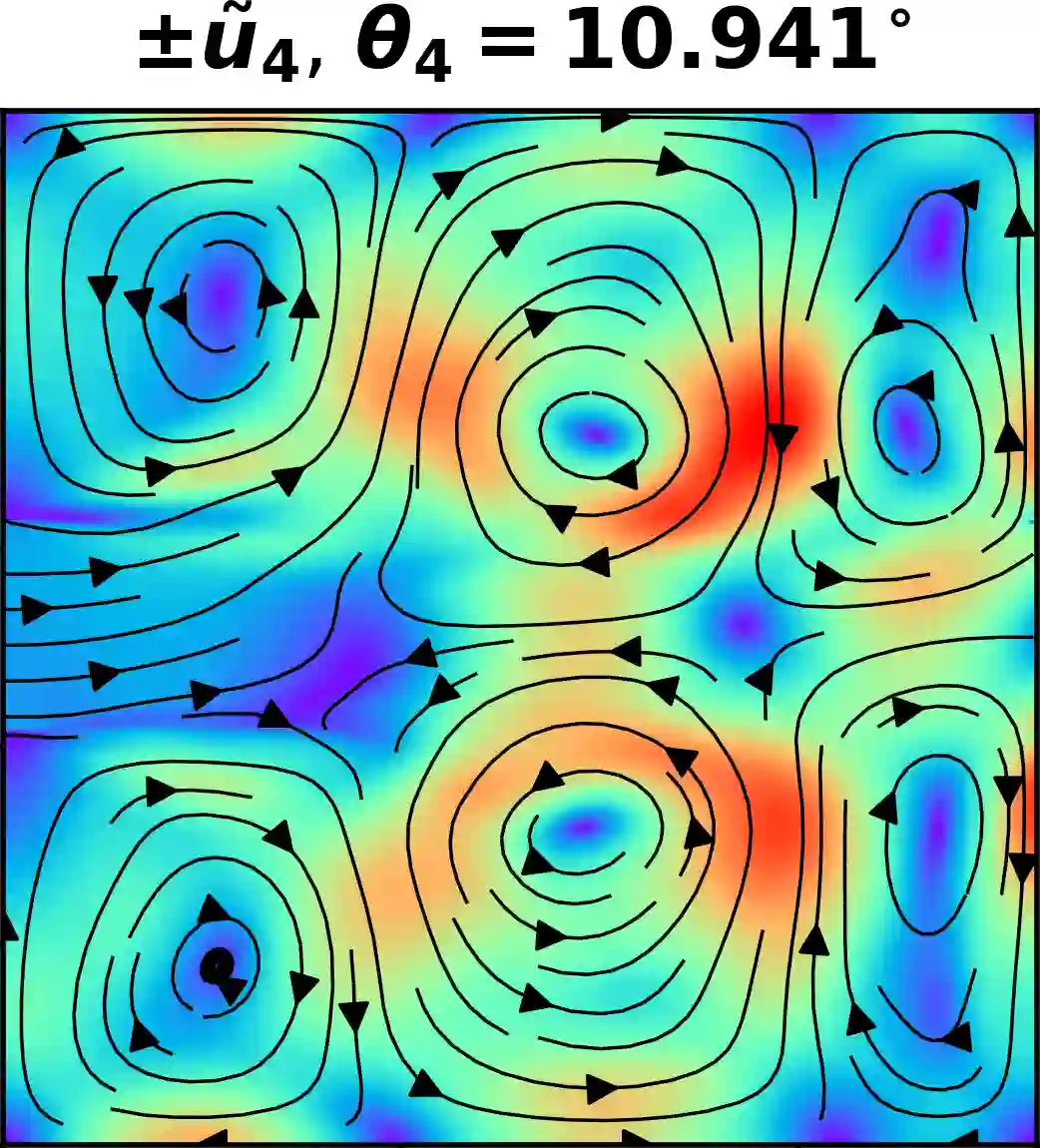
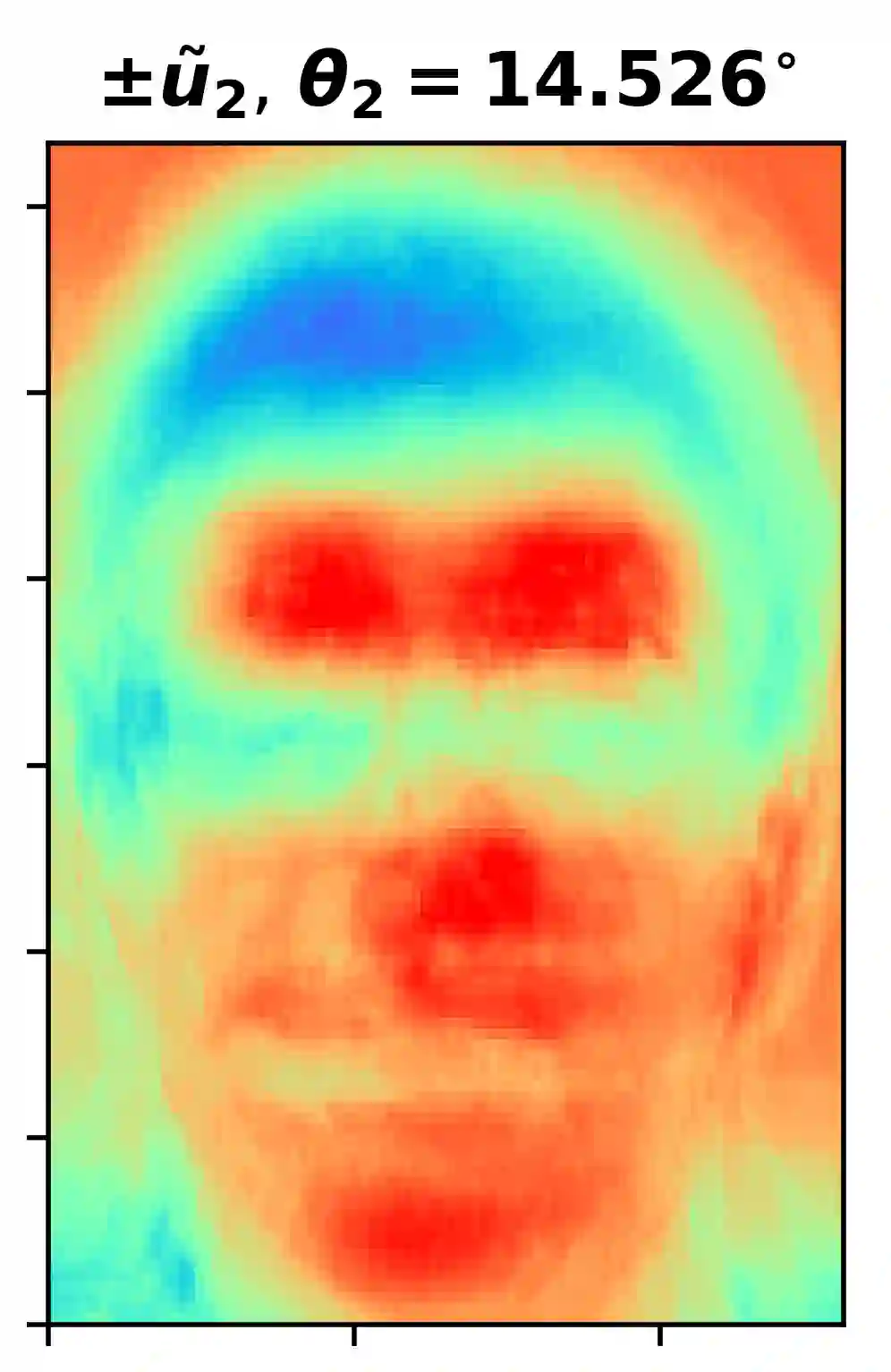
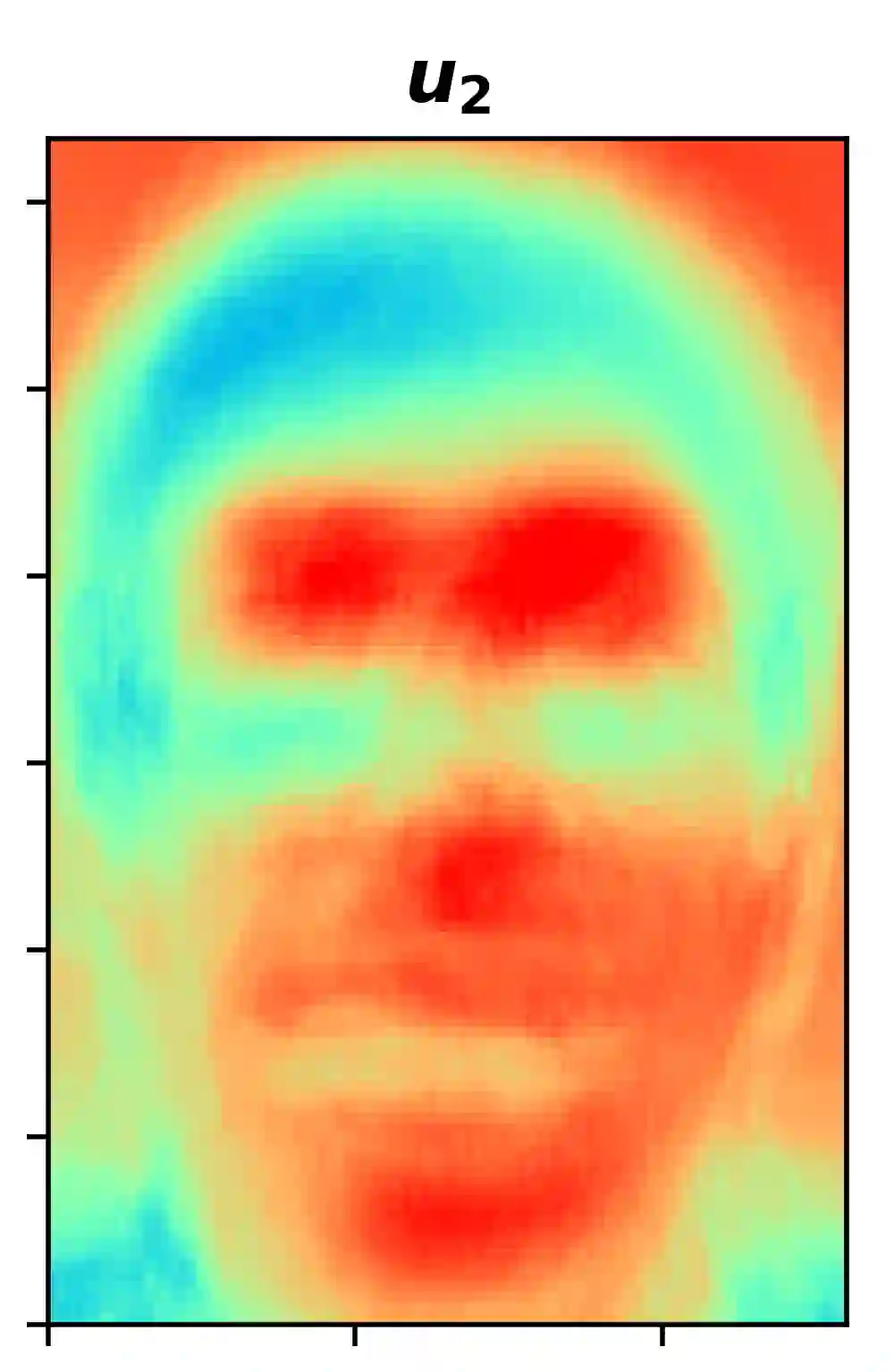
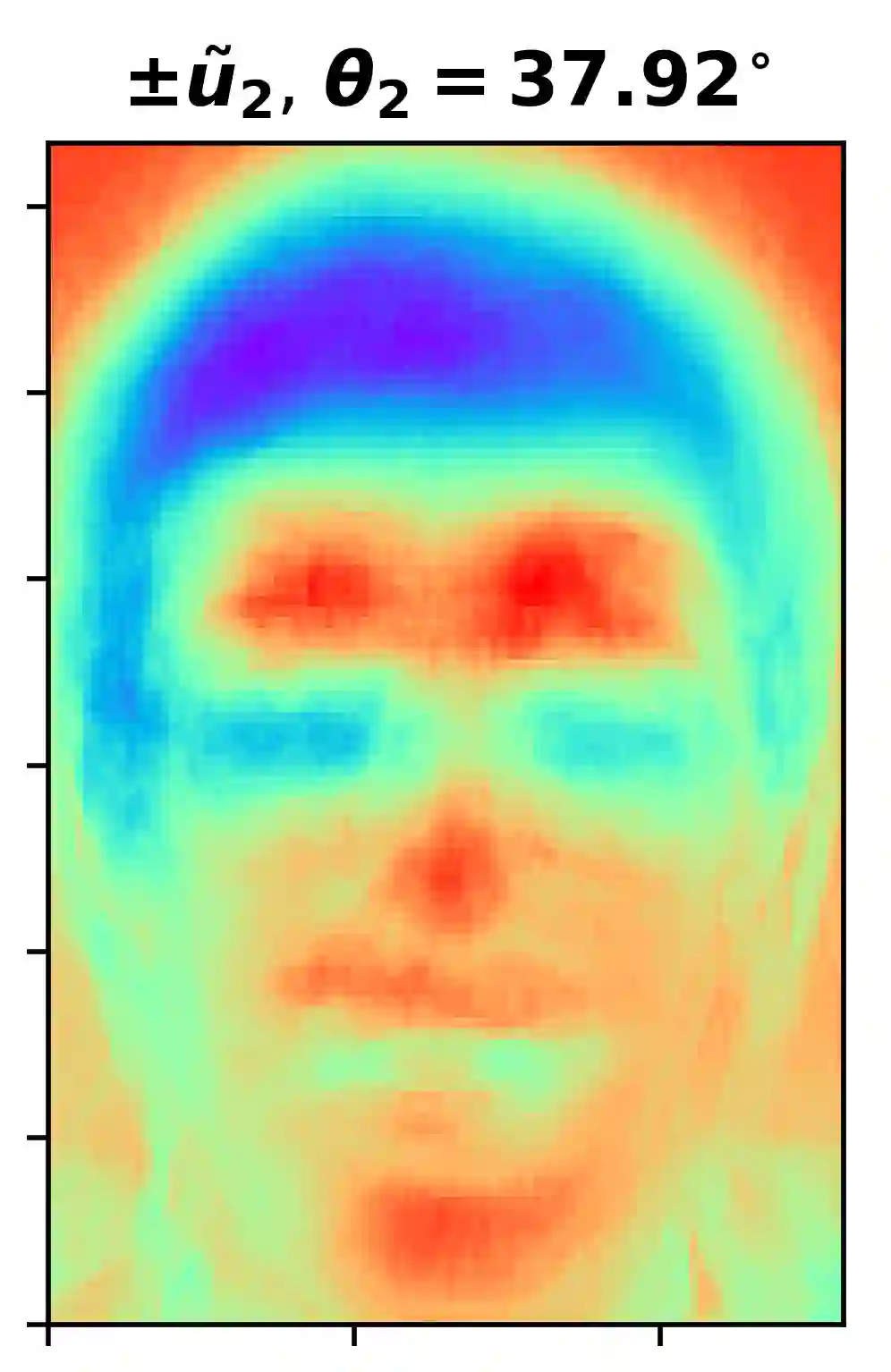
In this paper, we propose a computationally efficient iterative algorithm for proper orthogonal decomposition (POD) using random sampling based techniques. In this algorithm, additional rows and columns are sampled and a merging technique is used to update the dominant POD modes in each iteration. We derive bounds for the spectral norm of the error introduced by a series of merging operations. We use an existing theorem to get an approximate measure of the quality of subspaces obtained on convergence of the iteration. Results on various datasets indicate that the POD modes and/or the subspaces are approximated with excellent accuracy with a significant runtime improvement over computing the truncated SVD. We also propose a method to compute the POD modes of large matrices that do not fit in the RAM using this iterative sampling and merging algorithms.
翻译:在本文中,我们建议使用随机抽样技术,对正正正正正正正正正正正分解(POD)的计算高效迭代算法。在这一算法中,对额外的行和列进行抽样,并使用合并技术来更新每个迭代中占主导地位的 POD 模式。我们从一系列合并操作中引入的错误的光谱规范中得出界限。我们使用一个现有的理论来对迭代合并时获得的子空间的质量进行大致测量。关于各种数据集的结果表明,POD 模式和/或子空间的精确度非常接近,在计算短短的 SVD 时段上有很大的运行改进。我们还提出一种方法,用这种迭代抽样和合并算法来计算不适合在RAM 中的大型矩阵的 POD 模式。