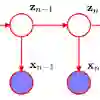
The conditional backward sampling particle filter (CBPF) is a powerful Markov chain Monte Carlo algorithm for general state space hidden Markov model smoothing. We show that, under a general (strong mixing) condition, its mixing time is upper bounded by $O(\log T)$ where $T$ is the time horizon. The result holds for a fixed number of particles $N$ which is sufficiently large (depending on the strong mixing constants), and therefore guarantees an overall computational complexity of $O(T\log T)$ f or general hidden Markov model smoothing. We provide an example which shows that the mixing time $O(\log T)$ is optimal. Our proof relies on analysis of a novel coupling of two CBPFs, which involves a maximal coupling of two particle systems at each time instant. The coupling is implementable, and can be used to construct unbiased, finite variance estimates of functionals which have arbitrary dependence on the latent state path, with expected $O(T \log T)$ cost. We also investigate related couplings, some of which have improved empirical behaviour.
翻译:暂无翻译