Design-Based Uncertainty for Quasi-Experiments

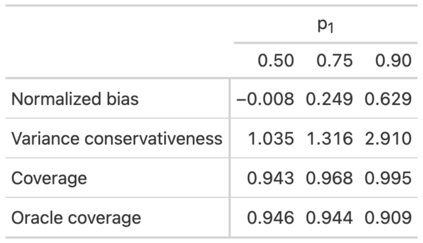
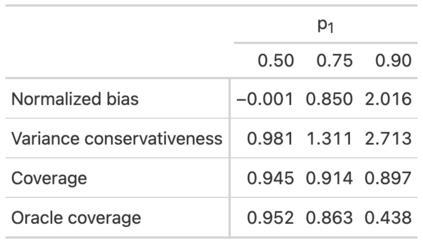
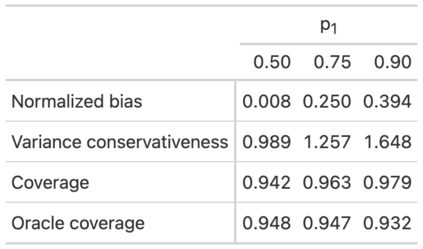
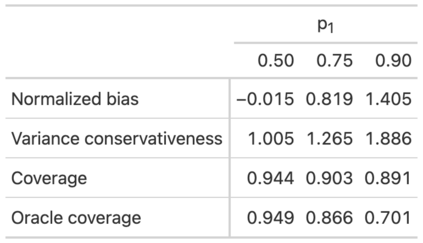
This paper develops a design-based theory of uncertainty that is suitable for analyzing quasi-experimental settings, such as difference-in-differences (DiD). A key feature of our framework is that each unit has an idiosyncratic treatment probability that is unknown to the researcher and may be related to the potential outcomes. We derive formulas for the bias of common estimators (including DiD), and provide conditions under which they are unbiased for an intrepretable causal estimand (e.g., analogs to the ATE or ATT). We further show that when the finite population is large, conventional standard errors are valid but typically conservative estimates of the variance of the estimator over the randomization distribution. An interesting feature of our framework is that conventional standard errors tend to become more conservative when treatment probabilities vary across units. This conservativeness helps to (partially) mitigate the undercoverage of confidence intervals when the estimator is biased. Thus, for example, confidence intervals for the DiD estimator can have correct coverage for the average treatment effect on the treated even if the parallel trends assumption does not hold exactly. We show that these dynamics can be important in simulations calibrated to real labor-market data. Our results also have implications for the appropriate level to cluster standard errors, and for the analysis of linear covariate adjustment and instrumental variables.