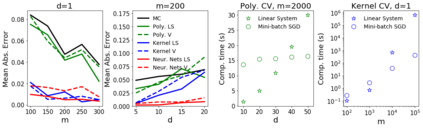
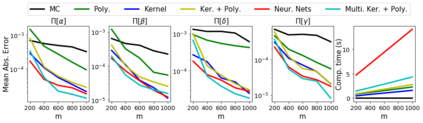
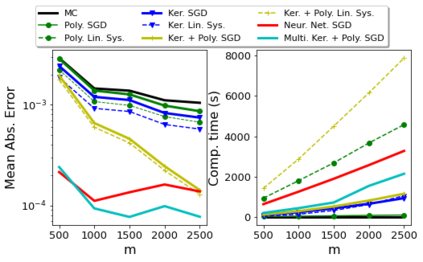
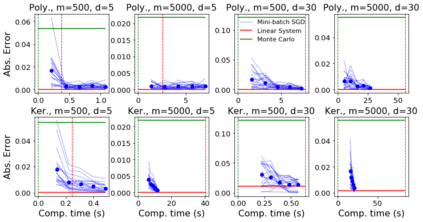
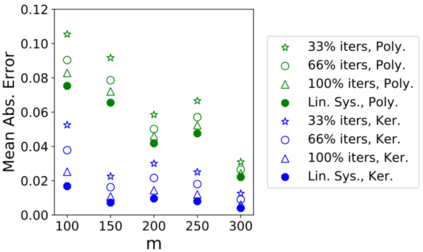
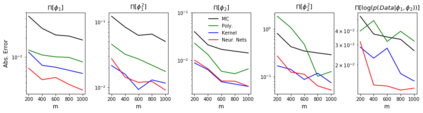
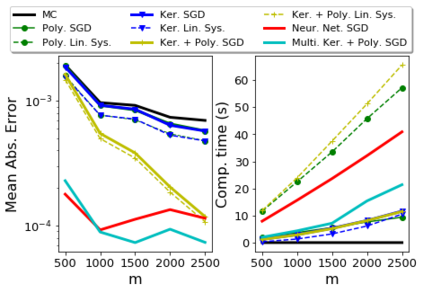
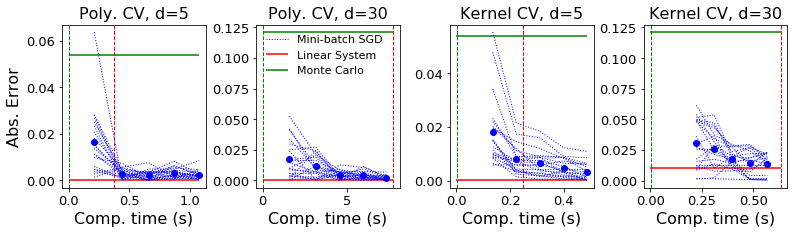
Control variates are a well-established tool to reduce the variance of Monte Carlo estimators. However, for large-scale problems including high-dimensional and large-sample settings, their advantages can be outweighed by a substantial computational cost. This paper considers control variates based on Stein operators, presenting a framework that encompasses and generalizes existing approaches that use polynomials, kernels and neural networks. A learning strategy based on minimising a variational objective through stochastic optimization is proposed, leading to scalable and effective control variates. Novel theoretical results are presented to provide insight into the variance reduction that can be achieved, and an empirical assessment, including applications to Bayesian inference, is provided in support.
翻译:控制变异是减少蒙特卡洛估计值差异的既定工具,但是,对于包括高维和大型抽样环境在内的大规模问题,其优势可以被大量计算成本所抵消。本文考虑了基于斯坦因操作员的控制变异,提出了一个框架,包含并概括了使用多球、内核和神经网络的现有方法。提出了基于通过随机优化最小化变异目标的学习战略,导致可缩放和有效的控制变异。提出了新理论结果,以深入了解可以实现的差异减少,并提供了经验评估,包括对贝叶斯推断的应用。