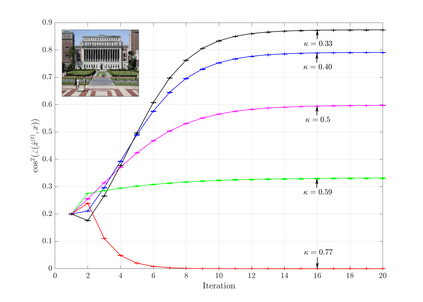
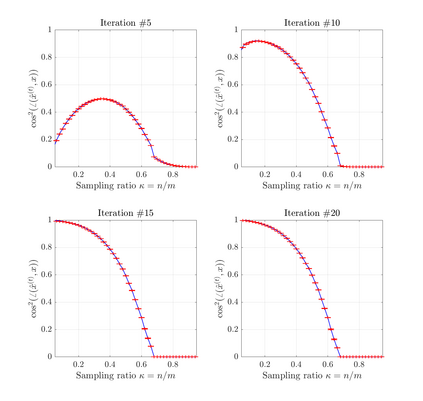
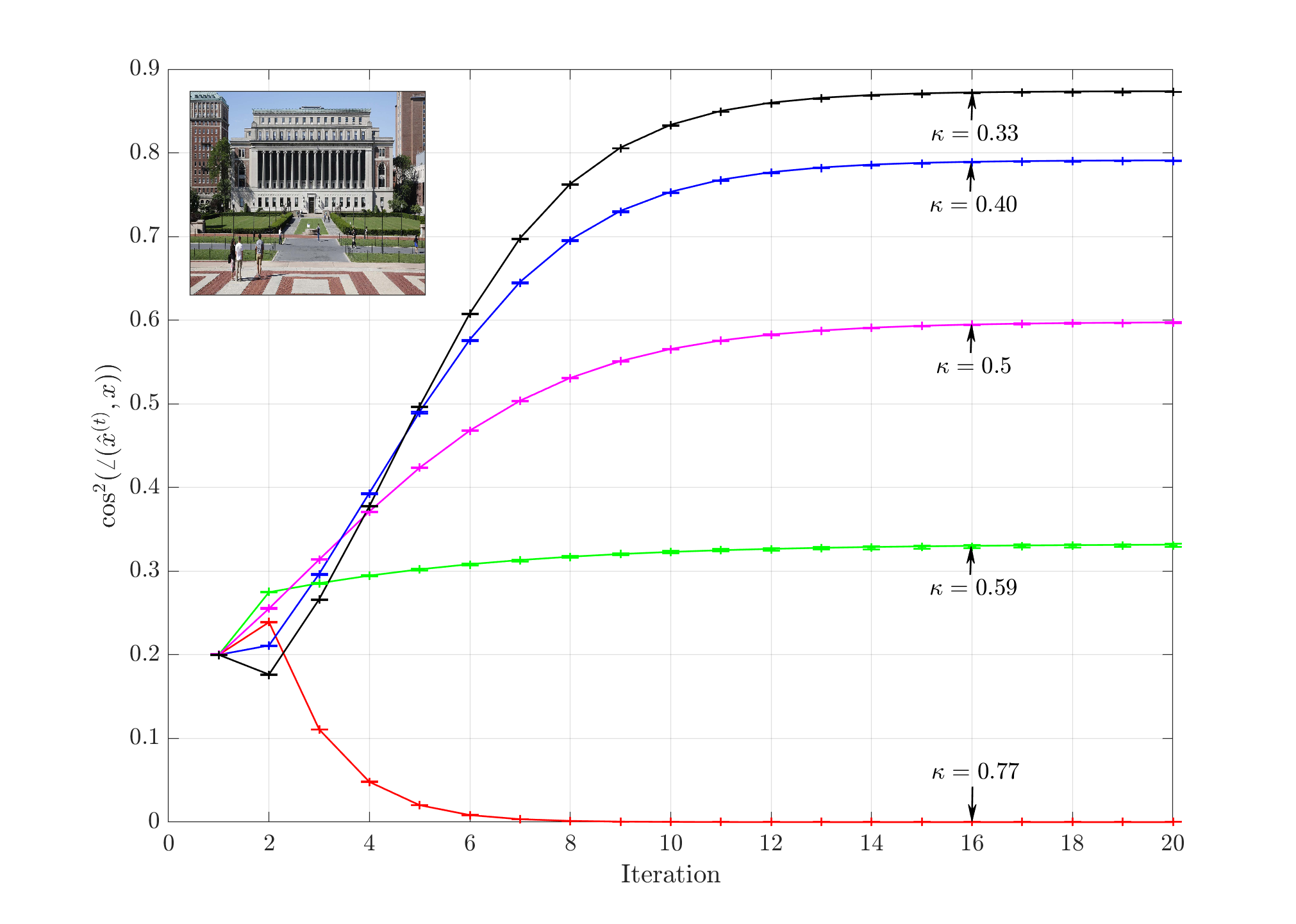
In the phase retrieval problem one seeks to recover an unknown $n$ dimensional signal vector $\mathbf{x}$ from $m$ measurements of the form $y_i = |(\mathbf{A} \mathbf{x})_i|$, where $\mathbf{A}$ denotes the sensing matrix. Many algorithms for this problem are based on approximate message passing. For these algorithms, it is known that if the sensing matrix $\mathbf{A}$ is generated by sub-sampling $n$ columns of a uniformly random (i.e., Haar distributed) orthogonal matrix, in the high dimensional asymptotic regime ($m,n \rightarrow \infty, n/m \rightarrow \kappa$), the dynamics of the algorithm are given by a deterministic recursion known as the state evolution. For a special class of linearized message-passing algorithms, we show that the state evolution is universal: it continues to hold even when $\mathbf{A}$ is generated by randomly sub-sampling columns of the Hadamard-Walsh matrix, provided the signal is drawn from a Gaussian prior.
翻译:在阶段检索问题中, 一个人试图从以$y_ i = {( mathbf{A}\ mathbff{x}}_ $ 美元表示感测母体。 这个问题的许多算法都以传递近似信息为基础。 对于这些算法, 众所周知, 如果感知母体 $mathbf{{A} 由以统一随机( e., Haar 分布) 或直方矩阵为单位的一列以美元为单位的子抽样取样生成, 以美元为单位, 以美元为单位, (m)\\ rightrow\ infty, n/m\rightbror\kappa$为单位。 对于这些算法来说, 许多算法的动力是由一种被称之为状态演进化的确定性递归来给出的。 对于一种特定的线性信息传输算, 我们表明, 状态进化是通用的: 即使由 $\\ {Hamar mas 所生成的螺旋轴, 仍由 irbromals robs pas roal pral traps 提供 roal prest exblasml- glasp adbs aslation aslations aslations 。