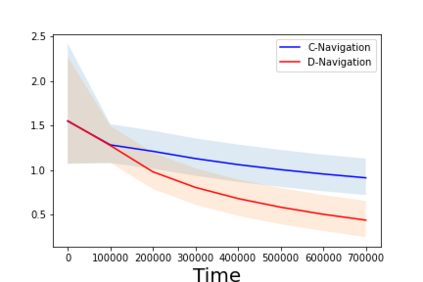
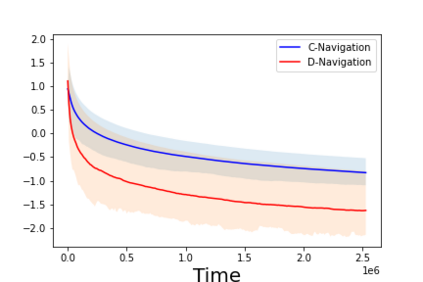
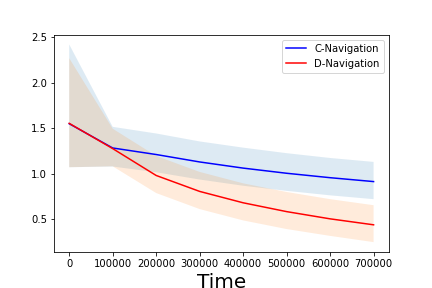
We investigate the classical active pure exploration problem in Markov Decision Processes, where the agent sequentially selects actions and, from the resulting system trajectory, aims at identifying the best policy as fast as possible. We propose a problem-dependent lower bound on the average number of steps required before a correct answer can be given with probability at least $1-\delta$. We further provide the first algorithm with an instance-specific sample complexity in this setting. This algorithm addresses the general case of communicating MDPs; we also propose a variant with a reduced exploration rate (and hence faster convergence) under an additional ergodicity assumption. This work extends previous results relative to the \emph{generative setting}~\cite{pmlr-v139-marjani21a}, where the agent could at each step query the random outcome of any (state, action) pair. In contrast, we show here how to deal with the \emph{navigation constraints}, induced by the \emph{online setting}. Our analysis relies on an ergodic theorem for non-homogeneous Markov chains which we consider of wide interest in the analysis of Markov Decision Processes.
翻译:在Markov决定过程中,我们调查典型的纯纯勘探问题,在这个过程中,代理人按顺序选择行动,并从由此产生的系统轨迹中,力求尽快确定最佳政策。我们建议对正确回答之前所需的平均步骤数量设定一个取决于问题的较低约束,概率至少为1美元-delta$。我们在此背景下进一步为第一个算法提供具体实例的样本复杂性。这种算法处理的是通信MDP的一般案例;我们还在另外的ergodicity假设下提出一个降低勘探率(并因此更快地趋同)的变量。这项工作扩展了与\emph{generative settle{cite{plr-plr-v139-marjani21a} 相比的先前结果,该代理每一步都可以查询任何(状态、动作)配对的随机结果。与此相反,我们在这里展示如何应对mph{navigation constrict},这是由 lemph{online setting}我们的分析依据一个非hogencyal Markov seconomical 分析的非荷利。