Finding Super-spreaders in Network Cascades

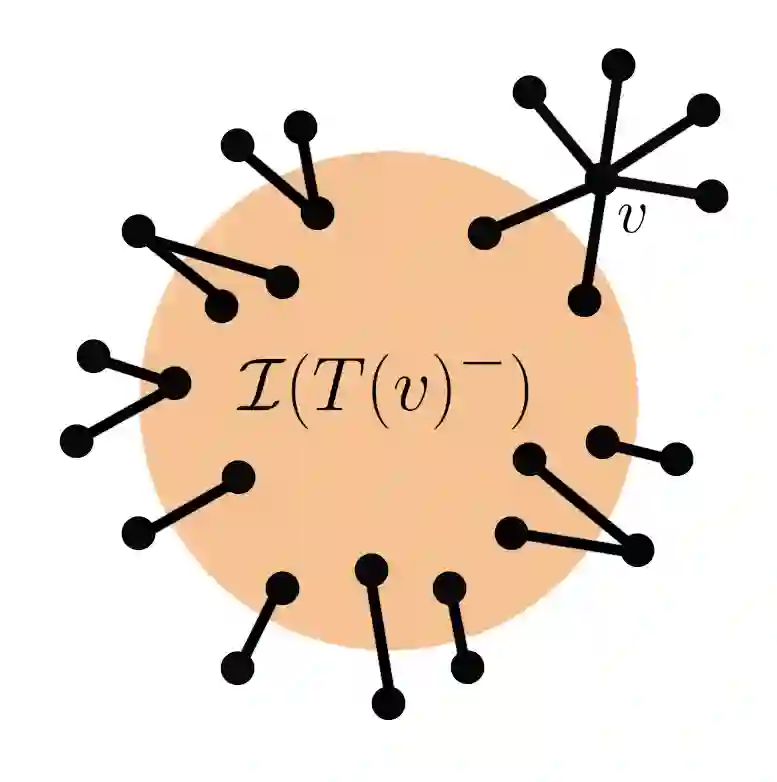
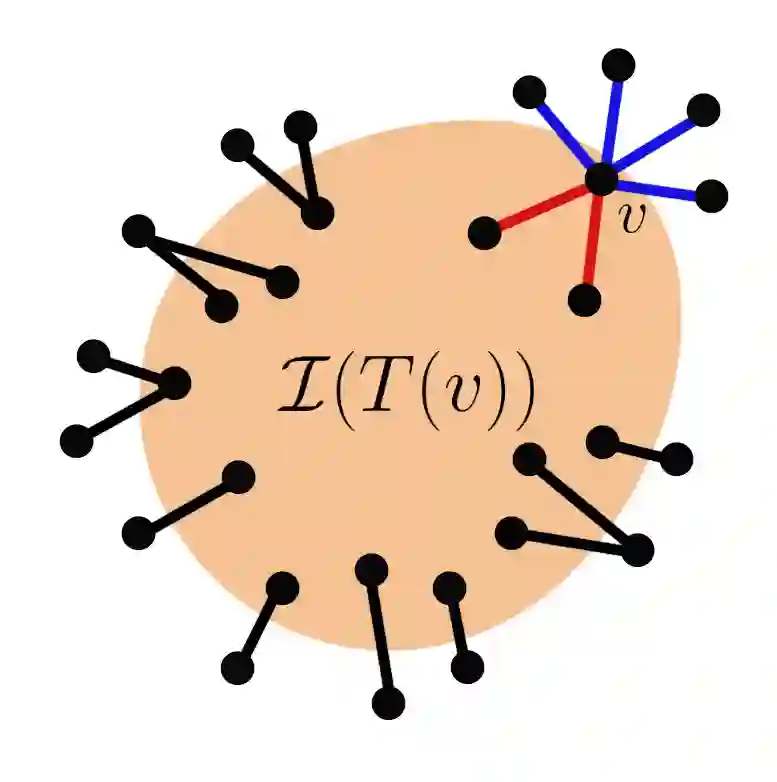
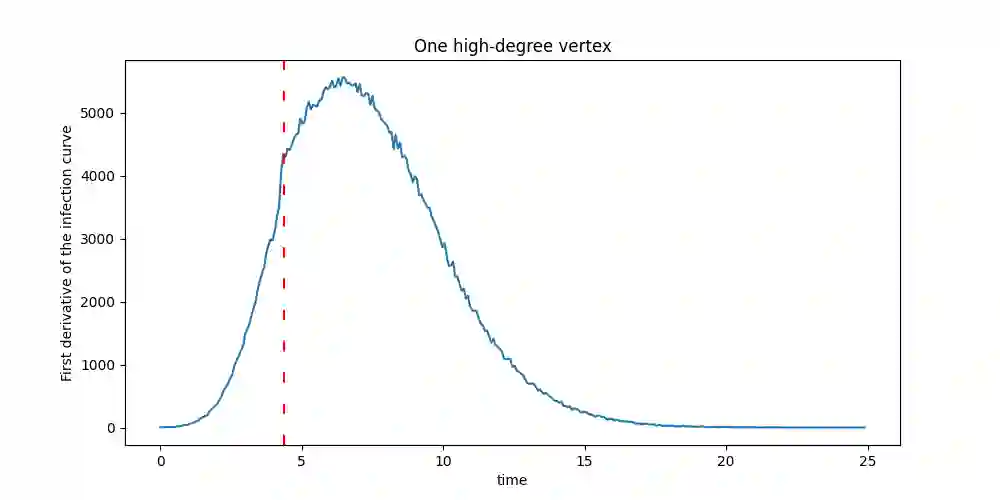
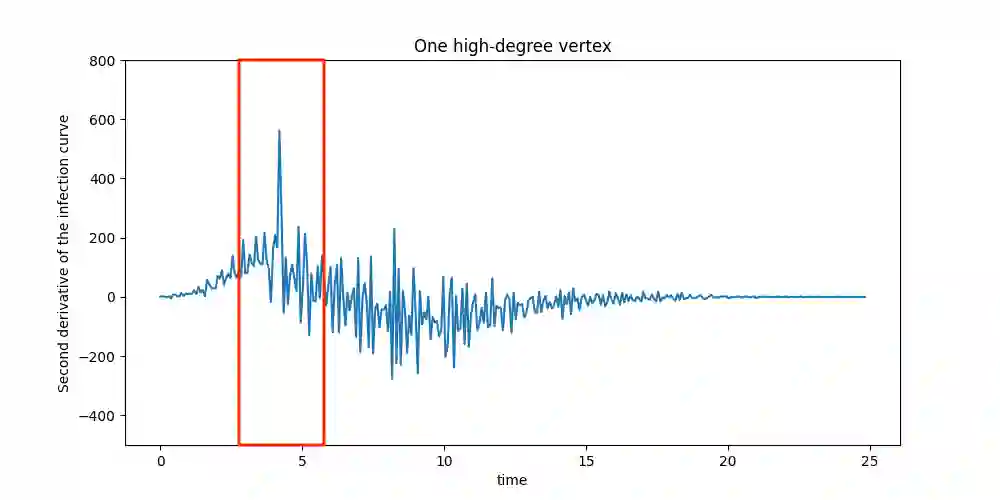
Suppose that a cascade (e.g., an epidemic) spreads on an unknown graph, and only the infection times of vertices are observed. What can be learned about the graph from the infection times caused by multiple distinct cascades? Most of the literature on this topic focuses on the task of recovering the entire graph, which requires $\Omega ( \log n)$ cascades for an $n$-vertex bounded degree graph. Here we ask a different question: can the important parts of the graph be estimated from just a few (i.e., constant number) of cascades, even as $n$ grows large? In this work, we focus on identifying super-spreaders (i.e., high-degree vertices) from infection times caused by a Susceptible-Infected process on a graph. Our first main result shows that vertices of degree greater than $n^{3/4}$ can indeed be estimated from a constant number of cascades. Our algorithm for doing so leverages a novel connection between vertex degrees and the second derivative of the cumulative infection curve. Conversely, we show that estimating vertices of degree smaller than $n^{1/2}$ requires at least $\log(n) / \log \log (n)$ cascades. Surprisingly, this matches (up to $\log \log n$ factors) the number of cascades needed to learn the \emph{entire} graph if it is a tree.