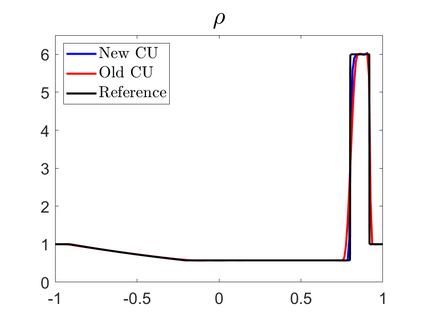
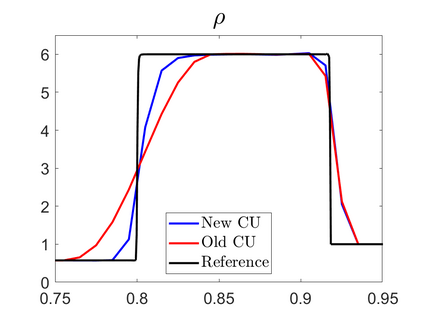
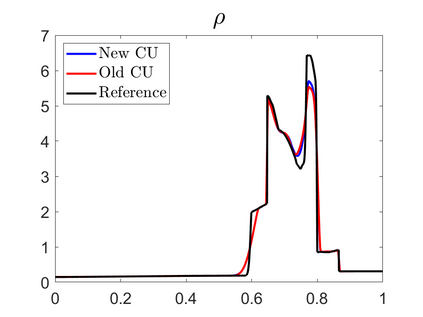
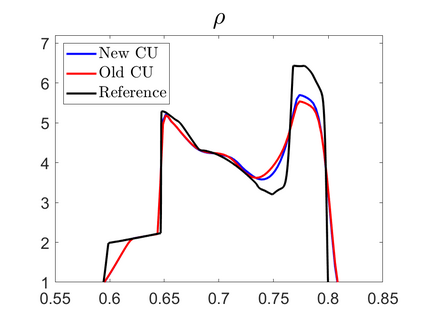
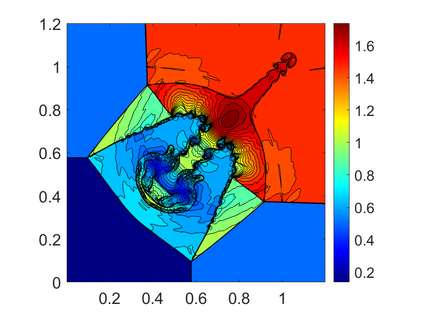
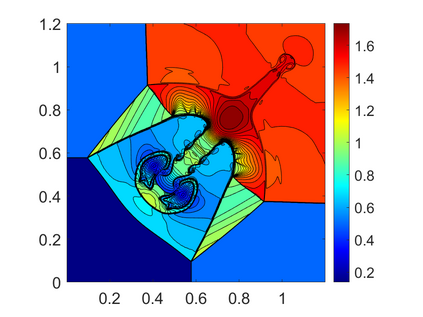
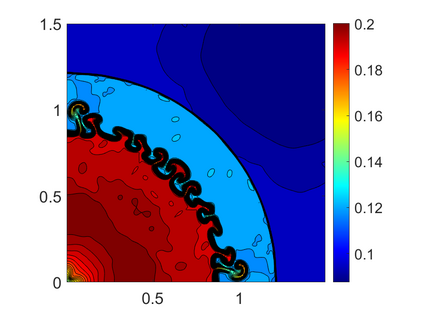
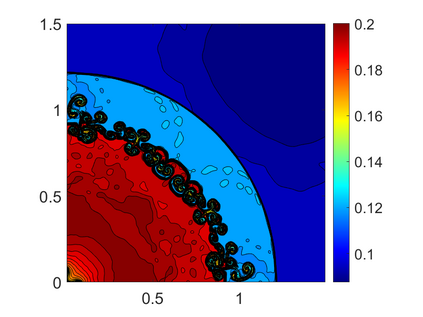
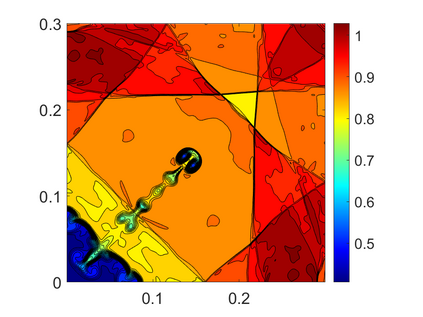
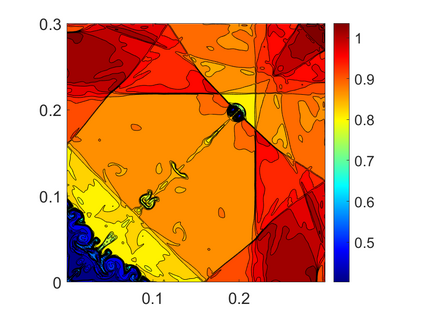
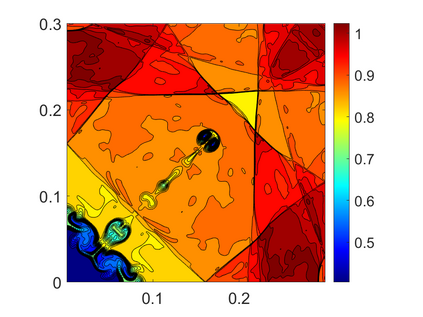
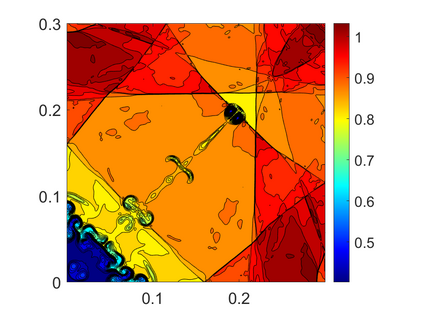
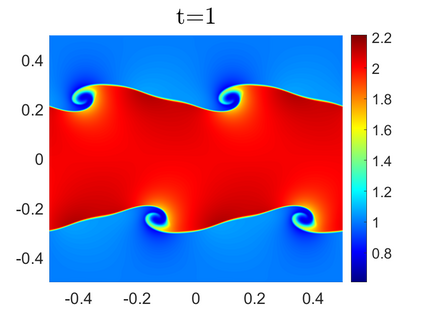
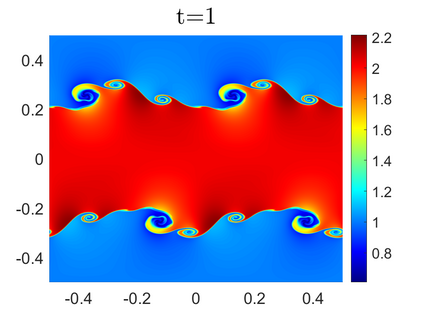
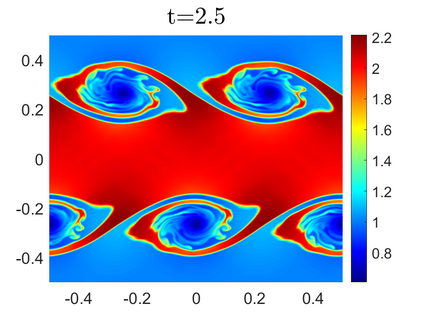
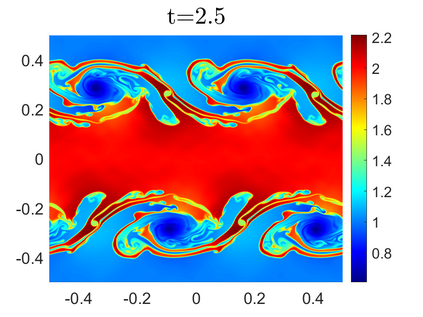
We propose novel less diffusive schemes for conservative one- and two-dimensional hyperbolic systems of nonlinear partial differential equations (PDEs). The main challenges in the development of accurate and robust numerical methods for the studied systems come from the complicated wave structures, such as shocks, rarefactions and contact discontinuities, arising even for smooth initial conditions. In order to reduce the diffusion in the original central-upwind schemes, we use a local characteristic decomposition procedure to develop a new class of central-upwind schemes. We apply the developed schemes to the one- and two-dimensional Euler equations of gas dynamics to illustrate the performance on a variety of examples. The obtained numerical results clearly demonstrate that the proposed new schemes outperform the original central-upwind schemes.
翻译:我们为保守的一维和二维非线性局部偏差等式双曲线系统提出了新的较不费劲的计划。为研究过的系统制定准确和稳健的数字方法的主要挑战来自复杂的波浪结构,例如冲击、稀有行为和接触不连续等,即使是在平滑的初始条件下也是如此。为了减少最初的中风计划的传播,我们使用当地特有的分解程序来开发一个新的中上风计划类别。我们对气体动态的一维和二维尤尔等式应用发达的计划来说明各种例子的性能。获得的数字结果清楚地表明,拟议的新计划优于原的中上风计划。